
ARITMETIKA AFÁZIÁBAN: ESETTANULMÁNY1
Bánréti Zoltán - Mészáros Éva
1. BEVEZETÉS
Jelen írás olyan esettanulmányt tartalmaz, mely egy afáziás személy vizsgálata alapján lehetőséget nyújt, egy - szerintünk -- érdekes probléma bemutatására. Felfedező szándékú kutatás (pilot study) volt a célunk, az adatok kis mennyisége még nem teszi lehetővé statisztikai analízisek végzését, szignifikancia viszonyok megállapítását. Nem vállalkoztunk a számtani, matematikai képességek bonyolult kérdésköreinek részletes elemzésére sem. Egyetlen aspektust kívánunk vizsgálni: a szerkezetfüggőségnek és a rekurziónak a számolási és a nyelvi-mondattani rendszerek közti lehetséges szétválását, disszociációját, és ennek alapján következtetni a két rendszer viszonyára a középsúlyos Broca afázia feltételei között.
A számok megértésének és használatának feltétele - többek között - a számfogalom megléte, a számok jelentésének megértése, egyszerű műveletek felismerése, a számtani szabályok, algoritmusok, „technikák” alkalmazása, valamint az információk fenntartása a rövid távú memóriában (Mantovan et al. 1999; Krajcsi 2003, Fedorenko et al. 2007). Az afázia körülményei között a figyelmi és a végrehajtó funkciók érintettsége eleve megnehezítheti ezeket a műveleteket. Ugyanakkor az afáziás nyelvi korlátozottság sajátosságai tanulságosak a nyelv és az aritmetika közti viszony szempontjából.
2. AZ fMRI VIZSGÁLATOK
2.1. A témakörünkbe vágó fMRI vizsgálatok azon az elgondoláson alapulnak, hogy amennyiben valamely agyi régió egyaránt támogatja mind a nyelvi mind az aritmetikai műveleteket, akkor mindkét funkció esetében aktivitást kell mutatnia. Amennyiben viszont szelektíven csak a nyelvi folyamatokat támogatja, akkor aktív lesz a nyelvi feldolgozás során, de nem, vagy kevésbé aktív az aritmetikai műveletek végzésekor. Megjegyzendő, hogy a ‘ nyelvi folyamatok’ kapcsán ezúttal a magasabb szintű nyelvi műveletekhez társuló agyi aktivitásokra gondolunk, a mondatok/megnyilatkozások jelentését feldolgozó, illetve a jelentéssel bíró mondatokat/megnyilatkozásokat produkáló műveletek agyi korrelátumaira. Az esettanulmányunkban nem foglalkozunk azon fMRI kutatásokkal, melyek a beszédhangok és az írásjelek elsődleges auditív illetve vizuális percepciójának a kezdeti analízisében résztvevő agyi régiókra irányulnak, illetve a beszédprodukció legvégső szakaszaiért felelős artikulációs-motoros agyi régiókra. A magasabb szintű nyelvi folyamatok közül elsősorban a szintaktikai műveletek lényegesek a tárgyalt probléma szempontjából.
Friederici et al. (2011) tanulmányában bemutatott fMRI vizsgálatok szerint a komplex, nem-nyelvi szekvenciák, többek között a matematikai-aritmetikai hierarchikus szerkezetek feldolgozásakor aktivációkat mutató régiók: baloldali homloklebeny elülső régióiban (anterior prefrontális kéregben), az ún. Brodmann area, ezentúl: BA 47 régió (a Broca terület előtt és alatt) valamint BA 45/elülső területe (a Broca terület elülső régiója) valamint a BA 10 területe (a homloklebeny legelején, jóval a Broca terület előtt) és a fali (parietális) kéreg. Ez a rendszer kevéssé automatizált és jelentős kognitív kontrolt igényel. A természetes nyelvi, rekurzív szintaktikai szerkezetek feldolgozásakor aktivációt mutató régiók: a BA 44 és BA 45/hátulsó területén (Broca terület hátulsó régiója). valamint a hátulsó, felső halántéklebeny (post STG = superior temporalis gyrus) régiói. Ez a feldolgozó rendszer - felnőtt személyek esetében - magas szinten automatizált, nem determinált kognitív kontroll által. A kétféle, hierarchikus szerkezeteket feldolgozó rendszer tehát különbözik egymástól a terület tekintetében és a kognitív kontroll fokában. Friederici és mtsai 2011 alábbi ábrában foglalja össze:

ábra. Az említett, fontosabb agyi régiók
(Az ábra felett említett BA-k (Brodmann area-k) megoszlásai sematikusan: piros színnel jelölve a Broca terület és környéke (nyelvi szintaxis és aritmetika), lila színnel a Broca terület alatti és előtti régió (aritmetika), fekete színnel BA 10 (aritmetika), kék színnel a fali lebeny (aritmetika), piros-sárga satírozás: a hátulsó felső halántéklebeny (nyelvi szintaxis és lexikon.). Megjegyzendő, hogy Friederici és munkatársai vizsgálatai szerint az alsó homloklebenyi barázda (=IFS: inferior frontal sulcus) a Broca területhez kapcsolódó munkamemória funkciókban aktív. A zöld színnel jelölt motoros kéregben a BA 6 és 4 régiók valamint a középső barázda (CS= central sulcus) az események szekvenciáinak feldolgozásakor mutattak aktivitást, de ezek jelen témánknál nem relevánsak).
A nyelvi és a matematikai szerkezetek feldolgozása során tehát egyaránt aktív a Broca terület, de eltérő részterületeken, a természetes nyelvi szintaxis esetében a BA 44 és a BA 45 hátulsó régiója, míg a matematikai-aritmetikai formulák feldolgozásakor a BA 44 és a BA 45 elülső régiója. A neuroanatómiai részletektől eltekintve, Friederici és munkatársai úgy összegeztek, hogy a nyelvi hierarchikus szerkezetek feldolgozása az alsó homloklebenyi agytekervény hátulsó részének aktivását váltja ki, míg a matematikai formulák feldolgozása az alsó homloklebenyi agytekervény elülső régióinak aktivitását. Továbbá a hátulsó, felső halántéklebeny (temporalis tekervény) aktivitását csak a természetes nyelvi szintaktikai szerkezetek feldolgozásakor mutatták ki, viszont a BA 47 terület (Broca terület előtt és alatt) valamint a fali lebeny (parietális kéreg) aktivitása a matematikai-aritmetikai feladatokhoz kötődött. Friederici és mtsai (2011) amellett érvelnek, hogy két, párhuzamos feldolgozó rendszerről van szó, az egyik erősen automatikus (természetes nyelvi hierarchikus szerkezetek feldolgozása), míg a másik kevésbé automatikus és kognitív kontrollt kíván (matematikai-aritmetikai és más hierarchikus szerkezetek feldolgozása). A két, párhuzamos, de eltérő lokalizációjú, más funkciójú és eltérő automatizáltságú és kontrolláltságú feldolgozó rendszer modelljét a Jeon - Friederici (2013), Friedrich - Friederici (2013) és Jeon - Friederici (2015) művekben bemutatott eredmények megerősítették és kiterjesztették.
3. A NYELVI HÁTTÉR KÉRDÉSE
3.1. Friederici képletek és számolási formulák feldolgozása során kapta a fenti eredményeket. De a numerikus kogníciónak két, különböző alaprendszerét azonosították. Az egyik a kevés alapelemből álló, egzakt számrendszer, amely, többek között, lehetővé teszi az objektumok mennyiségének eldöntését, pontos információkkal identitásukról és térbeli helyükről (Feigenson et al. (2004).
A másik alaprendszer a becslés, a megközelítő, nagyságbeli, térbeli analógiával működő, mennyiségbecslési rendszer, amely nagyobb halmazokra szolgáltat „zajos” becsléseket. Whalen et al. (1999). Az evolúciós aspektusok taglalását nem tekinthetjük feladatunknak. Pusztán megemlítjük, hogy klasszikus kutatások mutattak rá arra, hogy a kognitív architektúra felépülésében bizonyos fajta számolási képesség a nyelvtől függetlenül létrejöhet és fennmaradhat, de a nyelv lexikona és szintaxisa az egzakt számrendszereket támogatja (Butterworth, 1999).
A számnevek nyelvi rendszere nélkül a mennyiségek analóg, nagyságvezérelte becslései működhetnek. Híres példák ilyen rendszerekre a munduruku és a piraha nyelvek. A munduruku esetében 1-től 5-ig vannak számot jelentő szavak, e fölött a „néhány”, „sok”, „kis mennyiség” kifejezéseket használják, becslés jelleggel. A számot jelentő szavakat “körülbelül” értelemben használják, az „egy” és „kettő” szavakat kivéve (Pica - Leme - Izard et al. 2004). A pirahák az „egy”, „kettő” és „sok” kifejezéseket alkalmazzák. A “kettő” jelentésű szó mindig nagyobb mennyiségre vonatkozik, mint az “egy” (adott kontextusban), de az “egy”-et olyan kis mennyiségek jelölésére is használják, mint a 2 - 3 (Frank - Everett - Fedorenko, 2008). Vagyis a pirahában csak a 3-nál kevesebb elemből álló halmazokat lehet elvileg előszámlálni. Azért “elvileg”, mert a ”pontosan egy”-re nincsen kitüntetett szó, a ‘hói’: ‘egy’ az körülbelül egy-et, vagy kevés-t/ kicsi-t is jelent, és megakadályozza az egzakt számnévi kifejezések pontos fordítását a pirahára (Gordon, 2004, 10.). Ugyanakkor mindkét népcsoport felnőtt és gyermek tagjai az aránytörvénynek megfelelően oldottak meg egyszerű műveleteket, ami arra utal, hogy analóg nagyságreprezentációra alapozták számításaikat, az egzakt számrendszer helyett az analóg, nagyságreprezentáción alapuló becslési rendszer használata kerül előtérbe (Gordon, 2004, 1-10., Csépe - Győri - Ragó 2008, 250-251.).
Mivel a legtöbb kultúrában jelen van az egzakt mennyiségek reprezentálásának verbális lehetősége, ezért születtek olyan javaslatok, melyek szerint az egzakt aritmetika azon neurális rendszeren alapul, amely a nyelvi feldolgozás mögött áll (pld. Dehaene 2003). Idegi képalkotó kutatások és kétnyelvű beszélők vizsgálatai szolgáltattak a természetes nyelvi hátteret támogató adatokat például Dehaene - Cohen (1997), Dehaene - Spelke & Pinel. (1999), Stanescu-Cosson, - Pinel,-van de Moortele, et al. (2000), van Harskamp - Cipolotti. (2001), Delazer - Girelli – Graná et al. (2003).
Viszont az újabb kutatások, elsősorban az újabb fMRI vizsgálatok arra az eredményre jutottak, hogy a nyelvi és a számolási műveletek nem azonos, bár egymáshoz közel elhelyezkedő agyi régiókhoz kötődnek (pld. Friederici et al. 2011, Friedrich - Friederici 2013, Fedorenko - Behr -Kanwisher et al. 2011). Továbbá Monti - Parsons & Osherson et al. (2012) kutatása szerint a „nyelvi régiók” nem aktívak akkor, amikor a személy aritmetikai feladatokat old meg, hanem más agyi régiók aktiválódnak. Maruyama - Pallier - Jobert et al. (2012) az algebrai műveletek szintaktikai komplexitását különféleképpen változtatta, és ennek során a fali (parietális) lebenyben és a nyakszirti lebenyben (occipitális lebenyben) talált aktivációkat, de nem talált ilyeneket a homlok- és halántéklebenynek (fronto-temporális régióknak) a nyelvi rendszerhez kapcsolódó területén.
Az fMRI kutatások eredményei tehát abba az irányba mutatnak, hogy a magasabb szintű nyelvi feldolgozás során erős aktivációkat mutató agyi régiók nem általánosan aktívak, amikor aritmetikai problémák megoldása a feladat, a nyelvi feldolgozás és az aritmetikai feldolgozás agyi kapcsolatrendszerei elkülönülnek egymástól.
4. AGRAMMATIKUS AFÁZIA ÉS SZÁMOLÁS
4.1. Azon elméletek számára, melyek szerint a nyelvi rendszer van az egzakt számolási képesség mögött, a legnagyobb kihívást olyan empirikus adatok jelentik, melyek szerint afáziás személyek, a baloldali, a „nyelvi központokra” is kiterjedő agyi sérülés és ennek következtében létrejött agrammatikus afázia mellett is megőrzött egzakt aritmetikai képességeket mutattak. Ha ugyanis a nyelvi rendszer vagy annak valamely komponense kritikus az aritmetikai műveletek végzése számára, akkor az afáziás nyelvi korlátozottságnak az aritmetikai műveleteknél is deficithez kell vezetnie. Másfelől, ha a nyelvi rendszer nem szükségszerű komponense az aritmetikai folyamatoknak, akkor a nyelvi rendszer deficitje a nyelvi megértést és a produkciót érintheti, de az aritmetikai műveletek (és más kognitív rendszerek) épek maradhatnak.
Baldo - Donkers (2007) 63 főből álló, bal féltekei, cerebro-vaszkuláris sérülést szenvedett, középsúlyos afáziás csoportot vizsgálva, kettős disszociációkat, szétválásokat talált a nyelvi értés és az aritmetikai értés tekintetében a páciensek egy-egy csoportjánál, mégis eredményeik összességét úgy értelmezték, hogy a nyelvi és az aritmetikai folyamatok valamiképpen átfedik egymást, különösen az összeadás és a szorzás esetében. Viszont Varley és munkatársai (2005) a nyelvi és az aritmetikai értés és produkció afáziabeli szétválását másképpen értelmezték. Bemutatták, hogy súlyosan agrammatikus afáziás személyek képesek lehetnek az aritmetikai alapműveletek (összeadás, kivonás, osztás, szorzás törtszámokra is) helyes elvégzésére. Kutatásukban három agrammatikus afáziás személyt teszteltek. Valamennyien felsőfokú végzettségűek voltak. A teszteredmények szerint az agrammatikus afáziás személyek számolási műveletei, beleértve a rekurzív műveleteket és a hierarchikus szerkezetre való érzékenységet, épek maradtak, miközben középsúlyos agrammatikus afáziások voltak a CT eredmények és az állapotfelmérő tesztbeli eredményeik alapján egyaránt. Súlyos nyelvi-szintaktikai korlátozottságokat mutattak, találgatás szintű teljesítményt produkáltak az írott mondatok nyelvtani helyességét megítéltető tesztekben, aszintaktikus mondatértést mutattak. Spontán beszédprodukciójuk töredezett frázisokból, vagy azok összetevőiből állt. A három személy közül csak egy volt képes a beszédben használni a számok neveit, a többiek nem. Ugyanakkor a különböző mennyiségek és arányaik kalkulációja a tesztben épnek bizonyult mindhárom személynél. Vagyis, miközben a személyek a nyelvi-szintaktikai szerkezetek tekintetében súlyos agrammatizmust mutattak, addig a kötött sorrendű aritmetikai műveletek esetében a zárójelek képezte beágyazott műveleteket jól értették és alkalmazták. Nyelvi-szintaktikai szerkezetek esetében ez lehetetlen volt számukra.
4.2. Varley és munkatársai kutatási motivációja az volt, hogy a természetes nyelvek nyelvtana és az aritmetikai szerkezetek között bizonyos párhuzamosságok vannak. A számokat jelentő valamint a velük végzett műveleteket jelentő szavak alapokat adnak az egzakt mennyiségekkel történő számolásnak és az aritmetikai műveletek kódolásának. A nyelvi és az aritmetikai kifejezések absztrakt mintázatai között párhuzamosságok vannak. Ilyenek a rekurzivitás és a szerkezetfüggőség. Például a kivonás és az osztás „megfordításait” tartalmazó numerikus kifejezések (5 - 10 és 10 - 5; illetve 5 : 10 és 10 : 5) eredményének helyes kiszámolása vagy a zárójelek követése [5 × (6 + 2)] a kifejezés szerkezeti tulajdonságaira vonatkozó érzékenységet kíván. Hasonlóképpen a szabályok rekurzív alkalmazása az összetevők egy véges halmazából potenciálisan végtelen kimenet generálását engedi meg. Ez a természetes nyelvben és az aritmetikai-számolási nyelvben egyaránt megtalálható („A szomszédnak van egy vizslája, aminek van egy tálkája, aminek van egy füle”…; (((( 2 + 1) +1) +1) +1) + …. A nyelv és az aritmetika közti kölcsönös függés tetten érhető olyan tartalmakban is, mint a szorzótábla, amely matematikai tények verbális jellegű kódolása és tárolása a hosszú távú memóriában. Ennek a tartalma minimális komputációs terhelés mellett segédeszközként elérhető az új számolási feladatok megoldása közben, így csökkentheti a komputációs terhelést. A számolás ilyen műveletei a tanult verbális információk aktiválásán alapulnak, és ez ahhoz a feltételezéshez vezetett, hogy a szorzás művelete különösen érzékeny lehet az afáziás nyelvi korlátozottság fennállására (Lemer et al. 2003).
Az agrammatikus afáziás személyekkel végzett tesztelések után Varley et al. (2005), majd Zimmerer -Varley (2010) konkluziója az volt, hogy bár az aritmetikai műveleteket olyan folyamatok közvetítik, melyek a lexikai és a szintaktikai műveletekhez is szükségesek, mégis az egyedfejlődés felnőtt korára, az érett elme architektúrájában a számolás a nyelvtől függetlenül fenntartottá válhat. Az agrammatikus afáziában talált szétválások nem zárják ki azt, hogy a szintaxis és a lexikon alrendszerei támogathatják a számolást, még nyelvi zavarok mellett is.
Varley et al. (2005) kétféle magyarázati lehetőséget vet fel a nyelv szintaxisa és az aritmetika szintaxisának kapcsolatára. Az egyik szerint a két rendszer egymástól függetlenül működik, egyikük korlátozódása nem kell, hogy érintse a másikat. A másik magyarázat szerint létezik egy közös szintaktikai rendszer, amely megalapozza mind a nyelvet, mind az aritmetikát, ám az aritmetikai feldolgozás közvetlenül hozzáférhet ehhez a rendszerhez anélkül, hogy nyelvi formába fordítanák át kifejezéseiket.
5. A VIZSGÁLATUNK BEMUTATÁSA
Esettanulmányunk középpontjában az a kérdésfeltevés áll, hogy az aritmetikai műveletek olyan jegyei, mint a rekurzivitás és a hierarchikus szerkezeti jegyekre való érzékenység, a természetes nyelvi megfelelőik által determináltak, tőlük függenek vagy pedig egyfajta párhuzamosság jellemzi a két rendszer ilyen jegyeinek a viszonyát.
5.1. Az afáziás vizsgálati személy és a normál kontroll
Cs.: 36 éves, jobbkezes férfi, iskola: 16 év, építészmérnök. A tesztek felvétele az agyi történés után 25 hónappal ((2 év,1 hónappal) történt, a vizsgálati személy állapota stabil volt. A CT a bal oldali arteria cerebri media területen akut ischemiás stroke-ot mutatott. A beszédprodukció és a beszédértés képességét a Western Aphasia Battery (WAB) szűrőteszttel (magyarra adaptált változata: Osmánné Sági 1991 mértük fel2. A WAB tesztben kapott eredmények szerint a vizsgálati személy: Broca-afáziás súlyos agrammatizmussal. Az ún. AQ (aphasia quotient) = 54,4 volt (a maximális pontszám: 100). Alkalmaztuk a beszédértést vizsgáló Token tesztet is (magyarra adaptált változata Osmánné Sági 1994). A Token teszt eredménye: 13 pont volt (a maximális pontszám: 36), közepes értészavart mutatott.
Cs. részt vett a rekurzív tagmondat-beágyazási képességeket vizsgáló tesztünkben. Az ingeranyag, az eljárás és a választípusok nyelvi jegyeit részletesen bemutatjuk Bánréti - Mészáros (2011), valamint a Bánréti – Hoffmann - Vincze (2016) művekben. A tesztek során mindennapi élethelyzeteket mutató képeket prezentáltunk és kérdéseket tettünk fel a képen látható személyekre vonatkozóan, hogy azok Vajon mit gondolhatnak /akarhatnak /kérhetnek /mondhatnak a képen látható szituációban. A tesztet tanító fázis vezette be, ennek során a személyek megtanulták magát a feladatot, ennek részeként a lehetséges válaszokra vonatkozó példákat is, ezek rekurzív tagmondat-beágyazások, valamint a hogy kötőszóval kezdődő beágyazott tagmondatok voltak (utóbbiak a mátrix mondat nélkül). A lehetséges válaszok példái mindig 3. személyű igei inflexiót tartalmaztak. Cs. válaszaiból kitűnik, hogy megértette a tesztfeladatot, sőt bizonyos válaszadási stratégiát is alkalmazott. A kérdések azon nyelvi típusainál, melyek kifejezetten támogatták a rekurzív tagmondat-beágyazást tartalmazó válaszokat, vagy a hogy kötőszóval kezdődő tagmondatot tartalmazó válaszokat, Cs. mindig elkerülte a tagmondat-beágyazást, és nem próbálkozott egyetlen hogy kötőszóval kezdődő fragmentummal sem. Néhány példa Cs. válaszaiból:
A képen: A lány megmutatja a csokit a fiúnak
Kérdés: Vajon mire gondol a fiú?
Cs. válasza: Kérsz? Kérek!
A képen: A lány egy mérlegen áll
Kérdés: Vajon mire gondol a lány?
Cs. válasza: Mennyi most? Mennyi? Hát nem szabad! Lefogyok!
A képen: A lány megkéri a fiút, hogy vágjon kenyeret
Kérdés: Vajon mire kéri a lány a fiút?
Cs. válasza: Kenyér és segíts! Nem bírom!
A képen: A lány pénzt kér a fiútól
Kérdés:Mit mondhat a lány?
Cs. válasza: Ennyi nem elég! Pénz.
A képen: A férfi elkéri a kulcsot a hotel portástól.
Kérdés: Vajon mit mondhat a férfi a portásnak?
Cs. válasza: Számla. Hát nem! Számla.
A válaszok szintaktikai szerkezete nagyon egyszerű, fragmentált. A produkált megnyilatkozások maximum két szintaktikai főösszetevőből álltak, olykor csak egyszavas válaszok voltak. (A spontán beszédét tipikusan az egyszavas megnyilatkozások jellemezték). A Vajon mit gondolhatnak /akarhatnak /kérhetnek /mondhatnak kérdésre, 18 különböző kép kontextusában összesen 39 választ adott (egy-egy képnél több, különböző választ is mondott). Az agrammatikus afázia olyan jellegzetes tüneteit mutatta, mint az ige produkciójában, valamint a főnévi esetragok produkciójában fellépő hibák. A 39 válaszból 15 válaszban egyáltalán nem volt ige, utóbbiakban csak főnevet produkált, közülük 5 válaszban a tárgyeset helyett alanyesetű főnevet. További 24 válasza viszont tartalmazott igét, ezekben 2 felszólító mód-inflexió hiányt és 6 válaszban a tárgyeset helyett alanyesetű főnevet produkált.
Az igét tartalmazó tesztbeli válaszok tartalma releváns volt. Jellegzetességük az egyes szám első személyű személyrag, illetve második személyű rag használata. Ilyeneket a tesztet tanító fázisban egyáltalán nem alkalmaztunk, ezek az afáziás személy saját produktumai voltak. A válaszok általunk „szituatív kijelentések”-nek nevezett tartalmakat hordoztak, melyek az afáziás személynek a képen látható szereplő mentális állapotára vonatkozó tudatelméleti következtetéseit jelenítették meg. Az egyes szám első személyű igei inflexió használata a tudatelmélet szimulációs modelljének alkalmazását mutatja, a személy a képen szereplő ember szituációjába belehelyezkedve, szándékait „átélve” produkálja a szituatív kijelentéseket. Cs. ilyen válaszai a képen látható szituáció szempontjából korrektek voltak. Egyúttal lehetővé tették számára, hogy kikerülje a tagmondat-beágyazást tartalmazó szintaktikai szerkezetek produkcióját. Egyetlen, hogy kötőszóval kezdődő fragmentumot sem produkált, miközben mégis megválaszolta a kérdést és nagyon egyszerű szerkezetekkel kompenzálta a szintaktikai korlátozottságát. Bánréti-Hoffmann-Vincze (2016) kimutatta, hogy az elkerült komplex szintaktikai forma és az alkalmazott, szimulációs tudatelméleti következtetések közös vonása a rekurzivitás. Amíg a nyelvi-szintaktikai rekurziót követő tagmondat-beágyazások vagy pusztán a hogy kötőszós tagmondatok használata nem volt elérhető az afáziás személy számára, addig a tudatelméleti következtetés rekurzív „logikáját” képes volt alkalmazni és szituatív kijelentésekben produkálni. Bánréti-Hoffmann-Vincze (2016) a személyek szélesebb körét vizsgálva azt az eredményt kapta, miszerint a Broca afáziásoknak az XY mit gondolhat/akarhat/kérhet stb. kérdésekre adott válaszaiban a szituatív kijelentések gyakorisága szignifikánsan magasabb volt, mint a normál kontroll személyek válaszaiban való előfordulás (Bánréti és mtsai, 2016, p.9.). A kompenzációs stratégia lényege: egy csak korlátozottan vagy egyáltalán nem elérhető rekurzív rendszer helyett egy másik, elérhető rekurzív rendszer alkalmazása. A kompenzáló funkciójú rendszer kevésbé automatizált és nagyobb kognitív kontrollt kíván, mint az a rendszer, amit kompenzál (Bánréti és mtsai 2016, p. 19-20.).
Jelen esettanulmányunkban egy normál kontroll személy vett részt: Z., 42 éves, jobbkezes férfi, iskola: 16 év, foglalkozása: tanár.
5.2. A vizsgálati anyagok és módszerek
Az aritmetika tesztelésére Varley és munkatársai nyomán (2005) különböző, mindösszesen hétféle feladatot adtunk az afáziás vizsgálati személynek és a kontroll személynek. Az afáziás személy is írásban oldotta meg a feladatokat. Ez mindig egy-egy papírlapon történt, erre néha rész-számításokat is lejegyzett, de alapvetően fejben számolt. Az afáziás írásos feladatmegoldások jellegzetes típusait a Függelék-ben mutatjuk be,
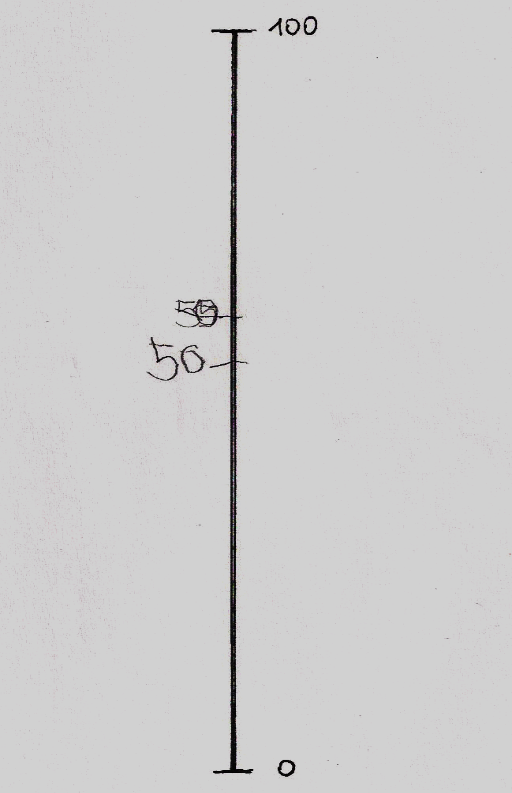
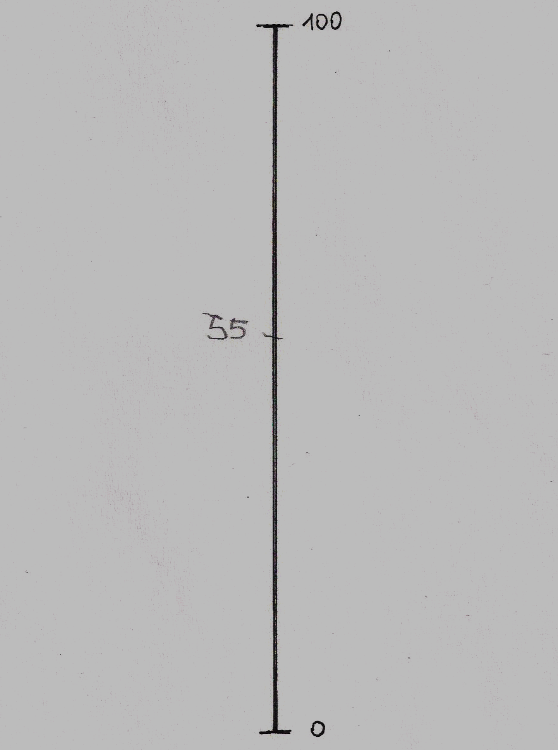
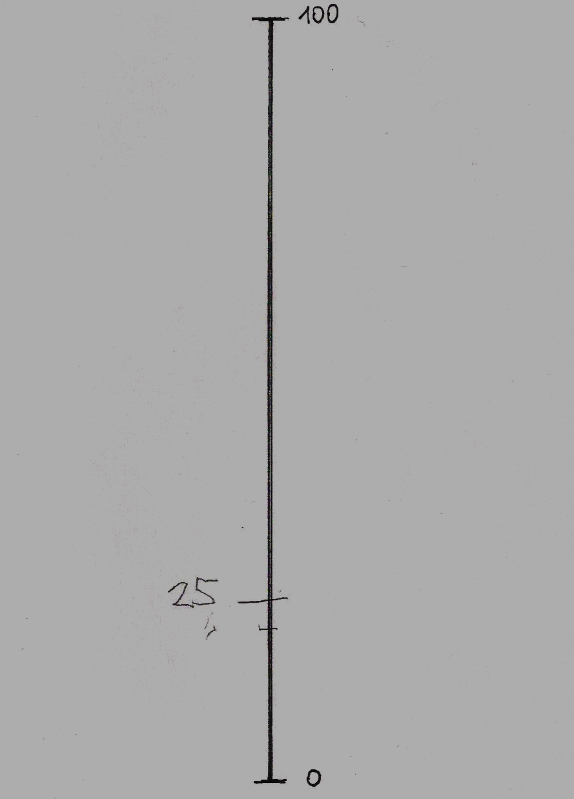
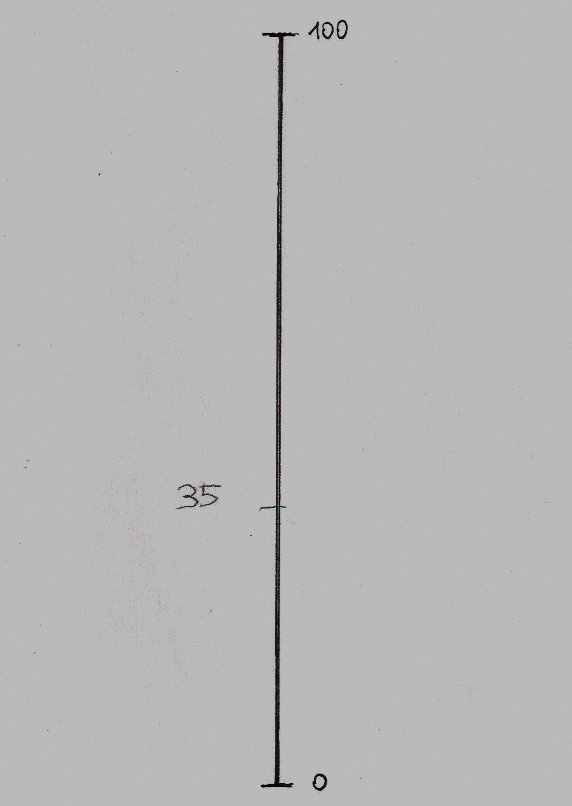
A számok nagyságának becslését kívánó feladathoz papírlapra rajzolt, 20 cm hosszú függőleges vonalon, azaz számegyenesen, melyen csak a két végpont: 0 és 100 értékei voltak megjelölve, 20 darab random sorrendben felolvasott szám megbecsült helyét kellett vízszintes vonallal megjelölni. A Broca afázia viszonylag jó értési teljesítményt enged meg, az egyenként felolvasott számok nem okoztak értési problémát. Ezt a feladat megoldásaiban is látható volt. A feladat azt vizsgálta, mennyiben ép a számok nagyságbeli viszonyaira vonatkozó fogalmak alkalmazása. (A számolási feladatlapot ld. a Mellékletben). A válasz akkor volt korrekt, ha a vonaljelölés 5 mm-en belül volt a megkívánt értékhelyhez képest.
A számolási feladatokban egy-, két- és háromjegyű számok összeadása, kivonása, szorzása és osztása szerepelt. A helyes eredmények ezekben a feladatokban pozitív egész számok voltak.
A műveletmegfordítási feladatban kéttagú számok kivonása és osztása szerepelt random sorrendben. A megfordítás arra vonatkozott, hogy a kivonás esetében először a nagyobb tagból történt a kisebb tag kivonása (pozitív szám lesz az eredmény, pld. 72 - 26), majd a kisebb számból a nagyobb kivonása (negatív szám lesz az eredmény, pld. 26 - 72). Az osztás esetében először a nagyobb számot kellett elosztani kisebbel (1-nél nagyobb szám lesz az eredmény, pld. 60 : 12), majd megfordítva, a kisebb számot kellett a nagyobbal osztani (1-nél kisebb lesz az eredmény, pld. 12 : 60). Mindezt három-három párban.
Három, majd négy számjeggyel végzendő számításokba zárójeleket helyeztünk el. Ezek szintaktikai funkciója az volt, hogy a zárójelen belüli műveletek elsőségét kívánták meg, majd ezek eredményének alkalmazását a rákövetkező műveletben. Nyolc ilyen feladat volt, melyekben, ha a vizsgálati személy, a zárójeleket figyelmen kívül hagyva a műveleti jelek puszta sorrendjét követte volna, téves eredményre jutott volna, mint például a 36 : (3 × 2) esetében. Volt további három olyan feladat is, melyekben a jelölt műveleti jelek puszta sorrendjének követése korrekt eredményt ad, mint például a 12 × (6 × 7) esetében. Egyszeres és kétszeres zárójelezések is alkalmaztunk. Az utóbbiak egy művelet tagjaként egy másik művelet beágyazását tartalmazták, amelybe egy újabb művelet volt beágyazva 2 x ((3 x 4) +10). Míg az egyszeres zárójelezések vagy a műveletsor bal szélén vagy a műveletsor második felében (jobb szélen végződve) fordultak elő, addig a kétszeres zárójelezések (8 db) a műveletsor jobb szélen végződve jelentek meg.
A zárójeles szerkezetek létrehozására vonatkozó feladatot az a kérés tartalmazta, miszerint a vizsgálati személy helyezzen el zárójeleket műveleti jelekkel kapcsolt négy számjegy sorozatában úgy, hogy az eltérő zárójelezések különböző eredményeket hozzanak létre, például: (6 + 2) × 5 + 8 = 48; 6 + (2 × 5) + 8 = 24; 6 + 2 × (5 + 8) = 32; ( 6 + 2) × (5 + 8) = 104 stb. A zárójelek alkalmazását a számolási feladatokban a rekurzív műveletvégzés jelölőinek tekintjük, mivel ekkor valamely műveletnek egy vagy több tagja (száma) maga is egy, a műveletbe rekurzív módon beágyazott számtani művelet eredménye3.
A számok végtelenségével kapcsolatos feladatban rekurzív számsorgenerálást kellett végeznie a vizsgálati személynek. A kiinduló feladata az volt, hogy írjon 1-nél nagyobb, de 2-nél kisebb számot, majd a választ követően egy újabb, a választottnál nagyobb, de a 2-nél kisebb számot kellett megadnia, a választ követően egy újabb, a választottnál nagyobb, de a 2-nél még mindig kisebb számot kellett megadnia, és így tovább - egyre növelve az értékeket anélkül, hogy a 2-őt elérné.
6. EREDMÉNYEK
6.1. Normál kontrollszemély
A normál kontroll személy számára a számolási feladatok nem jelentettek különösebb nehézséget, leszámítva azt, hogy viszonylag tartós figyelemkoncentrációt kívánt a teljesítésük. A szórványosan felbukkanó hibákat ez magyarázhatja.
Az 1. és a 2. táblázat az elvégzett feladatokban elkövetett hibák százalékos arányait mutatja (totál: az összes, elvégzett számítás, 0 = hibátlan számítások).
1. táblázat. Normál kontroll: az aritmetikai teszt elvégzett feladatainak eredményei a hibaarányok tekintetében (%)
| V. sz. | Számok nagyságának viszonyítása a számegyenesen n=20 |
Alapműveletek n=12/12/10/10 + - x : |
Kivonás, majd annak megfordítása, negatív szám az eredmény n=6 |
Osztás, majd annak megfordítása 1-nél kisebb szám az eredmény n=6 |
Végtelen számsor n=11 |
|||
|---|---|---|---|---|---|---|---|---|
| Z. | 1,9 | 0 | 0 | 0 | 10 | 0 | 0 | 0 |
2. táblázat. Normál kontroll: az aritmetikai teszt zárójeles feladatainak eredményei a hibaarányok tekintetében (%)
| V. sz. | Egyszeres zárójelezés n=20 |
Kétszeres zárójelezés n=8 |
Zárójelezés generálása n=25 |
Zárójelezés kiszámítása n=25 |
|---|---|---|---|---|
| Z. | 0 | 0 | 0 | 0 |
6.2. Az agrammatikus afáziás
Az afáziás személy a legtöbbször némán számolt, néhányszor akadozva verbalizálta a számolást, önellenőrzés végzésére is képes volt. A 3. és a 4. táblázat mutatja a hibák arányait, melyek a személy által elvégzett számításokban, a táblázatok az elkövetett hibák százalékos arányait mutatják, ahol a totál: az művelettípusban elvégzett összes számítási, a 0 hibaszázalék = hibátlan számítások).
3. táblázat. Afáziás személy: az aritmetikai teszt feladatainak eredményei a hibaarányok tekintetében (%)
| V. sz. | Számok nagyságának viszonyítása a számegyenesen n=20 |
Alapműveletek n=12/10/10/9 + - x : |
Kivonás, majd annak megfordítása, negatív szám az eredmény n=6 |
Osztás, majd annak megfordítása 1-nél kisebb szám az eredmény n=6 |
Végtelen számsor alkotása n=10 |
|||
|---|---|---|---|---|---|---|---|---|
| Cs., középsúlyos agrammatikus afáziás | 4,6 | 0 | 0 | 0 | 13 | 50 | 66,6 | 0 |
4. táblázat. Afáziás személy: aritmetikai teszt zárójeles feladatainak eredményei a hibaarányok tekintetében (%)
| V. sz. | Egyszeres zárójelezés kiszámolása n=9 |
Kétszeres zárójelezésbr n=3 |
Zárójelezés generálása n=9 |
Zárójelezés kiszámítása n=9 |
|---|---|---|---|---|
| Cs., középsúlyos agrammatikus afáziás | 42,8 | 33,3 | 0 | 100 |
6.2.1. Cs. a számegyenesen való tájékozódás során a megadott számértékek helyének az egyenesen történő jelölése kevés hibát tartalmazott, a hibaarány 4.6% volt. Ez csekély eltérés a normál kontrolltól. A számegyenesen vonallal jelölt értékek egymáshoz viszonyított, relatív sorrendjében nem tévedett, a hibaszázalékok abból adódnak, hogy a számokat ritkán, de 5 mm-nél nagyobb távolságra jelölte az adott érték helyéhez képest. (20 cm hosszú, puszta függőleges vonalról van szó, 2,5% eltérés = 5 mm eltérés, és csak az ezen felüli átlagos eltérést tekintettük hibának, így látható, hogy Cs.-nek az 5 mm-t meghaladó, átlagos eltérése durván átlag 4 mm volt).
6.2.2. Cs. az összeadás és kivonás hibátlan elvégzésére volt képes egy-, két- és háromjegyű számokkal egyaránt. Valamennyi ilyen feladatot megoldott.
Az osztásnál az elvégzett kilenc számolásból nyolcban jó eredményt adott, ezen belül két feladatnál az egész szám értéke volt pontos, a tizedes értéke hiányzott (elfogadtuk ezt a számolást), viszont két további feladatot elkerült, ezek háromjegyű osztandót és kétjegyű osztót tartalmaztak. Ilyet tartalmazó feladatból csak egyet oldott meg helyesen.
Az egy- és kétjegyű számokkal történő szorzás feladatait meg tudta oldani.
A kivonás tagjai sorrendjének megfordítása után negatív számot eredményező kivonásoknál nem ad pontos eredményeket, a negatív értéket magát helyesen rendeli hozzá a téves eredményekhez, ugyanennek a pozitív számot eredményező verzióit helyesen számolja ki. Az osztandó és az osztó sorrendjének megfordítása miatt 1-nél kisebb eredményt adó osztás feladatainál szintén nem ad jó eredményeket, az 1-nél nagyobb értékű eredményeket adó osztások közül két feladatnál számol jól (közülük az egyiknél hiányzik a tizedes értéke), egy továbbinál viszont a tizedes érték téves.
Három feladatban végzi el a tört számok összeadását, ennek komponenseként az eltérő nevezőjű törtek közös nevezőjének szorzással történő kiszámítását, valamint a megtalált közös nevezőhöz a számlálók értékeinek „felszorzását”, majd magát a törtszámok összeadásait. Két feladatban megoldása tökéletes, egy feladatban apró hiba van (a 8 és a 9 számjegy írásjegyének vizuális megkülönböztetésére vonatkozó kisebb zavar okán).
Az egyszeres zárójeles műveleteknél kilenc feladatot számolt ki, ebből öt feladatnál pontos és helyes az eredmény, négy feladatnál téves a végeredmény, de ezek közül három feladatban a zárójelen belüli rész-számítások helyesek, a végeredményben van tévedés.
A többszörösen zárójeles feladatok három-három művelet elvégzését kívánták, a zárójelek által megadott hierarchia szerint. Ezekből két feladatot teljesen kiszámolt úgy, hogy a három művelet pontosan követte a zárójelek kívánta hierarchiát, egy feladatnál pedig a két műveletet jól elvégezve a helyes részeredményig jutott. Ezúttal is jól követte a zárójelek adta műveleti sorrendet.
Cs. az általa generált, teljesen korrekt zárójeles formulák kiszámolására nem tett kísérletet.
A számok végtelenségének tudása megőrzött. Az egynél nagyobb, de kettőnél kisebb számok sorozatát helyesen generálja, a rekurzív szabályt felismeri és produkálja.
7. MEGBESZÉLÉS
7.1. A nyelvi erőforrások korlátozottsága
Cs. az aritmetikai műveletek kapcsán igénybe vehető nyelvi források tekintetében többfajta lexikai aktivációs korlátozottságot is mutatott.
Számolás közben gyakran félhangosan olvasta a számjegyeket, közülük a 9-et először 8-ként olvasta négy alkalommal is, de minden esetben saját maga kijavította a ténylegesen printelt 9-re. A félhangosan felolvasás során a helyi értékeknek a verbális jelölőinél szüneteket tartva hezitált, pld.: "nyolc…száz... nem!, nyolc…VAN ...hat". Vagy: „ (az eredmény): tizen... kettő, öö három, öö négy, ..négy! (ti. 14). Mindig eljutott a számjegy helyes nevéhez, át tudta kódolni a vizuális bemenetet verbálisra.
A műveletek közül a + jelnek és a - jelnek produkálta a neveit: („plusz”-nak, és „mínusz”-nak nevezte őket. Az osztás és a szorzás jeleinek a verbális megfelelőit (nevét) spontán módon nem tudta produkálni, az A x B valamint az C : D műveleteket úgy nevezte, hogy „A és B”, „C és D”. Az osztás, szorzás szavakat a vizsgálatvezető általi kimondásuk után meg tudta ismételni, de önállóan egyiket sem használta sem főnévi funkcióban, sem igenévi funkcióban (v.ö. A szorozva B-vel, C osztva D-vel kifejezéseket soha nem említette). Ugyanakkor a szorzásnak és az osztásnak a szimbolikus jeleit megértette és az általuk jelölt műveleteit el tudta végezni. A szorzási és osztási műveleteinek eredmények sok esetben pontosak voltak, ha nem is mindig.
A törtszámok neveit nem tudta produkálni, nem mondott „egyharmad, kéthatod neveket az 1/3, 2/6 számjegyek kapcsán, mikor kértük, mondja el, miképpen számolt, hanem így nevezte őket: „1 tört 3”, „2 tört 6,” stb. Ugyanakkor a törtszámokkal végzett összeadási és kivonási műveletei helyesek voltak, ezek során önállóan és helyesen alkalmazta a közös nevezőre hozást, tehát osztott, szorzott és összeadott, anélkül, hogy a műveletek nevét - a plusz-t kivéve - produkálni tudta volna.
A zárójel kifejezést nem használta sem a számolási sem a zárójelezéseket kérő feladatok félhangos elolvasása, illetve elvégzése alkalmainál. A zárójelek által megkívánt műveleti hierarchiát követő lépéseket viszont el tudta végezni.
7.2. A korlátozottságok hatásai
Cs. válaszmintázataiban három fő hatás figyelhető meg.
7.2.1. A komplexitási hatás: melynek tényezői a számjegy nagysága, az egy- vagy kétjegyű számokkal jobban számolt, mint a háromjegyűekkel, (a háromjegyű osztandót és kétjegyű osztót tartalmazó osztásokat elkerülte, viszont az összeadást és kivonást háromjegyű számokkal is jól végezte), magának a műveletnek a komplexitása (korlátozottságok a negatív számok és az 1-nél kisebb értékek eseteiben, a hibaarány emelkedése a zárójeles feladatok kiszámolásában). Hibátlanok voltak a pozitív egész számokkal végzett puszta összeadás és kivonás, valamint a zárójelet nem tartalmazó feladatokban a szorzás műveletei. Ezektől elmaradt az osztás eredményessége. Érdekes módon a törtszámok összeadásának komponensenként alkalmazott szorzásnál csak egyetlen apró hibát vétett. A komplexitási hatás masszív jelenléte a középsúlyos agrammatikus afázia körülményei között természetesen nem meglepő.
7.2.2. A második hatás a számok nagyságának adott tartományon belül történő becslésére vonatkozó képesség épen maradása. Cs. hibaaránya 4,6% volt, ami csekély eltérés a normál kontrolltól. Ez azt jelenti, hogy Cs. számolási műveleteket végző képessége komolyabban károsodott, mint a számok nagyságának adott tartományon belüli becslésének a képessége. Azt mondhatjuk, hogy a számszimbólumokkal jelölt mennyiségek értése megőrzött volt, és analóg módon, helyesen kifejezett.
7.2.3. A harmadik hatás: a rekurzív funkciók épsége. Ezt tesztelték a számok végtelen sorának alkotását kívánó feladatok és a zárójelek generálása megadott szám- és műveletsorra, többszörös zárójelezés elvégzését is kérő feladatok. E két feladatban a vizsgálati személy hibátlan teljesítményt nyújtott. Képes volt olyan számsorokat és olyan műveleti konstrukciókat képezni, melyek rekurzív módon tartalmaztak további számsorokat illetve műveleteket. Cs. a rekurzív szabály alkalmazása tekintetében adott hibátlan megoldásokat, viszont az önmaga által generált formula értékének aktuális kiszámolásába nem fogott bele, azt túlságosan nehéznek érezte (a zárójeles feladatok kiszámolása – komplexitásuk miatt – eleve nehezebb volt).
7.3. Azt találjuk tehát, hogy a középsúlyos agrammatikus Broca afáziás személy esetében az elvégezhető számolási műveletek komplexitása korlátozott, de ép a számok nagysága egymáshoz viszonyításának a képessége, valamint komplexitási limit mellett az egy- és kétjegyű, pozitív egész számokkal végzett alapműveletek és a rekurzív számsorok és műveletek produkciójára vonatkozó képesség. Utóbbiakat a zárójeles összetett sémaként, konstrukcióként produkálta, elkerülve ezeknek a komplex konstrukcióknak az aktuális értékekre történő kiszámítási műveleteit.
Ezek a disszociációk különösen annak fényében érdekesek, hogy korábbi vizsgálatainkban Broca-afázia körülményei között a nyelvi-szintaktikai rekurzió súlyos korlátozottsága mellett a rekurzív tudatelméleti következtetések épségét találtuk (Bánréti-Hoffmann-Vincze,2016). Az afáziás személy aritmetikai teljesítménye is mutat korlátozottságot, de ezek nem magukat az alapműveleteket, hanem az azok összetettebb változatait érintik. A számoláshoz elengedhetetlenül szükséges verbális nyelvi források korlátozottságai (lexikai és szintaktikai aktivációk zavarai) hibákhoz, zavarokhoz vezethetnek a komplexebb számításokban, de nem teszik elérhetetlenné azokat.
Említettük, hogy a nyelv és az aritmetika közti kölcsönös függések tetten érhető olyan tartalmakban is, mint a „szorzótábla”, ami verbálisan tárolt a hosszú távú memóriában. Ez tetszőleges, új számolási feladatok eredményeit automatikusan nem előlegezheti meg, az új számítási feladatokban segédeszközként, kontrollálóként használható. Lemer - Dehaene -Spelke - Cohen (2003) azt feltételezi, hogy az afáziás nyelvi korlátozottság a szorzást érinti legsúlyosabban. A mi vizsgálatunk adatai ezt nem támasztják alá.
8. ÖSSZEFOGLALÁS
Esettanulmányunk, a benne foglalt kutatás - az adatok kis mennyisége okán- óvatos következtetéseket enged csak meg. Hipotézisünk az volt, hogy a nyelvi és az aritmetikai kifejezések absztrakt mintázatai között olyan párhuzamosságok vannak, mint a rekurzivitás és a szerkezetfüggőség. Összefoglaltuk a nyelv és a számolás neurológiai hátterére vonatkozó fMRI vizsgálatokat, melyek szerint a nyelvi folyamatokban aktivitást mutató agyi régiók nem egyeznek meg az aritmetikai műveleteknél aktív régiókkal. A lokalitásbeli eltérés mellett a releváns agyi régiók funkcióiban is van különbség, miszerint a számokkal végzett műveletek produkciója és feldolgozása olyan agyi régiókhoz kötött, melyek -- a természetes nyelvi-szintaktikai feldolgozáshoz képest -- kevésbé automatizált, explicitebb és erősebb kognitív kontrollt tartalmazó folyamatokat vezérelnek. (Egy számolási művelet újra meg újra - „természetes módon” - lefuttatható, részműveletekre bontható, ellenőrizhető kontroll számításokkal).
A nyelvtől elkülönülten fenntartott aritmetika mellett szóló érveket jelentenek azon középsúlyos, agrammatikus afáziás állapotok is, melyekben a nyelvi (elsősorban szintaktikai és lexikai) folyamatok és az aritmetika szétválnak, az előbbiek erős korlátozottsága mellett az utóbbiak lényegesen jobb állapotot mutatnak, az alapvető műveleti funkcióikat illetően épen megőrzöttek.
Esettanulmányunkban jellemzett agrammatikus afáziás személy ilyen állapotot mutat. Eredményeink Zimmerer-Varley (2010) modelljét támogatják, mely szerint létezik egy közös szintaktikai rendszer, amely megalapozza mind a nyelvet, mind az aritmetikát, de felnőtt korban a számolás a nyelvtől elkülönülten fenntartott. Természetesen a modellépítéshez az afáziás személyek szélesebb körét fogjuk majd bevonni az aritmetikai képességeik tesztelésébe.
Köszönetnyilvánítás
Köszönettel tartozunk a vizsgálatban részt vett személyeknek.
Hivatkozások
Ansari, Daniel - Donlan, Chris - Thomas, Michael - Ewing, Sandra - Peen, Tiffany - Karmiloff-Smith, Annette 2003. What makes counting count? Verbal and visuo-spatial contributions to typical and atypical number development. Journal of Experimental Child Psychology 85: 50-62.
Baldo, Juliana - Dronkers, Nina. 2007. Neural correlates of arithmetic and language comprehension: a commonsubstrate? Neuropsychologia 45: 229-235.
Bánréti Zoltán - Hoffmann Ildikó - Vincze Veronika 2016. Recursive Subsystems in Aphasia and Alzheimer's Disease: Case Studies in Syntax and Theory of Mind, Frontiers in Psychology. 7:405. doi: 10.3389/fpsyg.2016.00405
Bánréti Zoltán - Mészáros Éva 2011. Szintaktikai rekurzió afáziában. Szerk.: Kenesei I. - Bartos H., Általános Nyelvészeti tanulmányok XXIII. 191-226.
Butterworth, Brian 1999. The Mathematical Brain. New York. Macmillan.
Cohen, Laurent - Dehaene, Stanislas - Chochon, Florence - Lehericy, Stéphane - Naccache, Lionel 2000. Language and calculation within the parietal lobe: A combined cognitive, anatomical and fMRI study. Neuropsychologia 38: 1426-1440.
Csépe Valéria, Győri Miklós, Ragó Anett 2008. Általános pszichológia 1-3. Nyelv, tudat, gondolkodás, Osiris Kiadó 2008. 250-251.
Dehaene, Stanislas - Cohen, Laurent. 1997. Cerebral pathways for calculation: double dissociation between rote verbal and quantitative knowledge of arithmetic. Cortex 33: 219-250.
Dehaene, Stanislas - Piazza, Manuela - Pinel, Philippe - Cohen, Laurent 2003. Three parietal circuits for number processing. Cognitive Neuropsychology 20: 487-506.
Dehaene, Stanislas - Spelke, Elizabeth - Pinel, Philippe - Stanescu-Cosson, Ruxandra - Tsivkin, Sanna 1999. Sources of mathematical thinking: Behavioral and brain-imaging evidence. Science 284: 970-974.
Dehaene, Stanislas - Cohen, Laurent. 1997. Cerebral pathways for calculation: double dissociation between rote verbal and quantitative knowledge of arithmetic. Cortex 33: 219-250.
Dehaene, Stanislas. 2003. The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends Cogn. Sci. 7: 145-147.
Delazer, Margarete - Girelli, Luisa - Graná, Alessia - Domash, Frank 2003. Number processing and calculation - - normative data from healthy adults. Clin. Neuropsychol. 17: 331-350.
Fedorenko, Evelina - Behr, Michael - Kanwisher, Nancy 2011. Functional specificity for high-level linguistic processing in the human brain. Proc.Natl. Acad. Sci.U.S.A. 108: 16428-16433.
Fedorenko, Evelina - Gibson, Edward - Rohde, Douglas 2007. The nature of working memory in linguistic, arithmetic and spatial integration processes. Journal of Memory and Language 56: 246-269.
Feigenson, Lisa - Dehaene, Stanislas - Spelke, Elisabeth 2004. Core systems of number. Trends Cogn. Sci. 8: 307-314.
Frank, Michael - Everett, Daniel - Fedorenko, Evelina - Gibson, Edward 2008. Number as a cognitive technology: evidence from Pirah˜a language and cognition. Cognition 108: 819-824.
Friederici, Angela - D. Jörg Bahlmann - Roland Friedrich - Michiru Makuuchi 2011. The Neural Basis of Recursion and Complex Syntactic Hierarchy, Biolinguistics 5.1-2: 087-104, 2011. http://www.biolinguistics.eu
Friedrich, Roland, M - Friederici, Angela 2013. Mathematical Logic in the Human Brain: Semantics, PLoS ONE 8(8): 10.1371/annotation/c08ee740-5917-4096-97e9-378ae5be1208. https://doi.org/10.1371/annotation/c08ee740-5917-4096-97e9-378ae5be1208
Gordon, Peter 2004. Numerical Cognition Without Words: Evidence from Amazonia, www.sciencexpress.org / 19 August 2004 / Page 1 - 10. 1126/science.1094492
Jeon, Hyeon-Ae - Friederici, Angela 2013. Two principles of organization in the prefrontal cortex are cognitive hierarchy and degree of automaticity. Nature Communications. 4: 2041. PMID 23787807 DOI: 10.1038/ncomms3041
Jeon, Hyeon-Ae - Friederici, Angela 2015. Degree of automaticity and the prefrontal cortex, Trends in Cognitive Sciences, Vol 19:5 244-250.
Krajcsi Attila 2003. Numerikus képességek. Erdélyi Pszichológiai Szemle 4/4: 331-382.
Lemer, Cathy - Dehaene, Stanislas - Spelke, Elizabeth - Cohen, Laurent 2003. Neuropsychologia 41: 1942-1958.
Maruyama, Masaki - Pallier, Christopher - Jobert, Antoinette - Sigman, Mariano, Dehaene, Stanislas 2012. The cortical representation of simple mathematical expressions. Neuroimage 61: 1444-1460.
Monti, Martin M- Parsons, Lawrence - Osherson, Daniel, S. 2012. Thought beyond language: neural dissociation of algebra and natural language. Psychol. Sci. 23: 914-922.
Osmánné Sági Judit 1991. Az afázia diagnózisa és klasszifikációja. Ideggyógyászati Szemle 44: 339-362.
Osmánné Sági Judit 1994. A De Renzi, D., Vignolo, M. beszédmegértési teszt adaptációjának eredményei. Ideggyógyászati Szemle 52: 300-332.
Pesenti, Mauro - Thioux, Marc - Seron, Xavier - De Volder, Anne 2000. Neuroanatomical substrate of Arabic number processing, numerical comparison and simple addition: A PET study. Journal of Cognitive Neuroscience 12: 461-479.
Pica, Pierre - Leme, Cathy - Izard, Veronique - Dehaene, Stanislas 2004. Exact and approximate arithmetic in an Amazonian indigene group. Science 306: 499-503.
Stanescu-Cosson, Ruxandra - Pinel, Philippe - van de Moortele, Pierre-Francois - Le Bihan, Denis - Cohen, Laurent - Dehaene, Stanislas 2000. Understanding dissociations in dyscalculia: A brain imaging study of the impact of number size on the cerebral networks for exact and approximate calculation. Brain 123: 2240-2255.
Van Harskamp, Natasja - Cipolotti, Lisa 2001. Selective impairments for addition, subtraction and multiplication. Implications for the organisation of arithmetical facts. Cortex 37: 363-388.
Varley, Rosemary A. - Klessinger, Nicolai - Romanowski, Charles - Siegal, Michael 2005. Agrammatic but numerate. Psychology PNAS Edition.
Whalen, Jhon - Gallistei, C.R. - Gelman, Rochel. 1999. Nonverbal counting in humans: the psychophysics of number representation. Psychol. Sci. 10: 130-137.
Zimmerer, Vitor - Valrey, Rosemary 2010. Recursion in severe agrammatism. In Hulst, H. (ed.): Recursion and Human Langauge. Studies in Generatív Grammar. Walter de Gruyter. 393-405.
FÜGGELÉK
PÉLDÁK AZ AFÁZIÁS VIZSGÁLATI SZEMÉLY FELADATMEGOLDÁSAIBÓL
SZÁMOK NAGYSÁGÁNAK VISZONYAI A SZÁMEGYENESEN
Minden kijelölés külön, független lapon történt, egyszerre mindig csak egyetlen, aktuális számegyenest látott a vizsgálati személy.

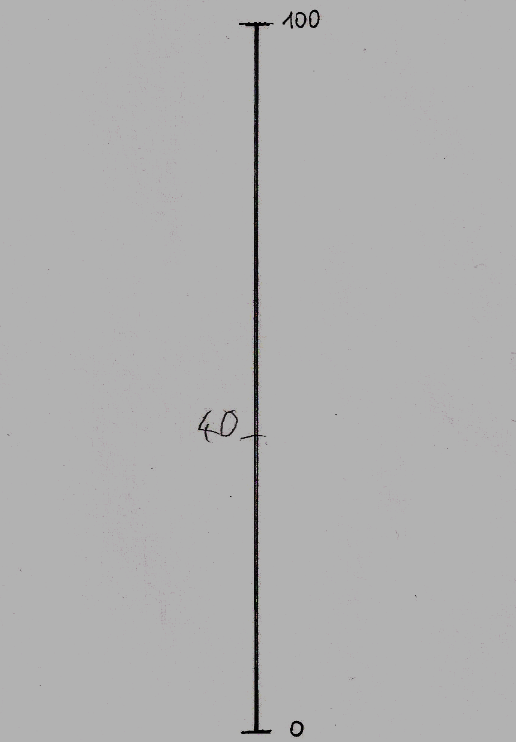


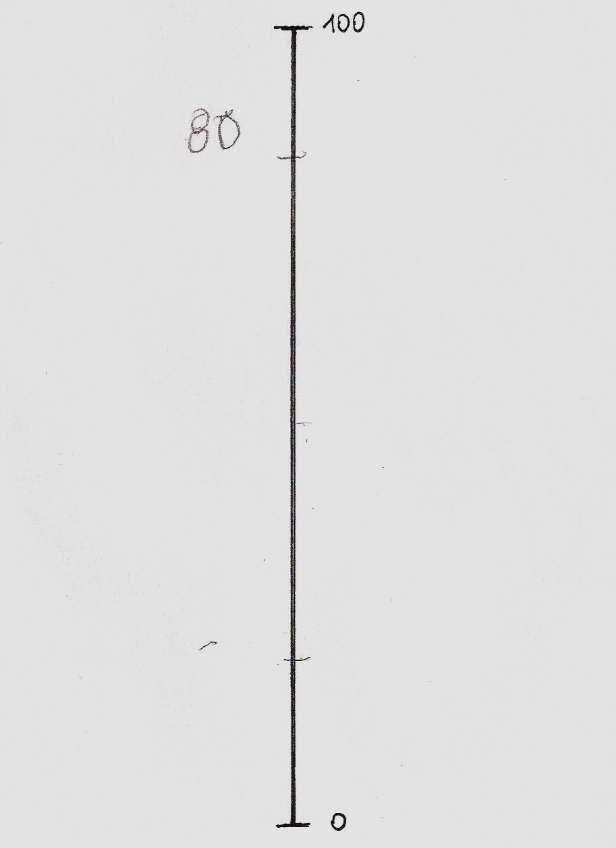

ALAPMŰVELETEK: ÖSSZEADÁS, KIVONÁS, SZORZÁS, OSZTÁS


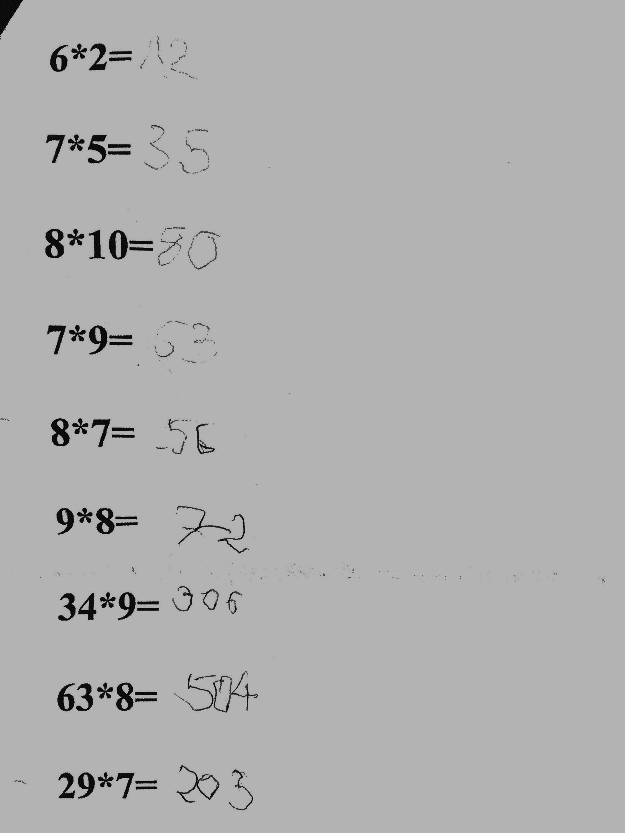
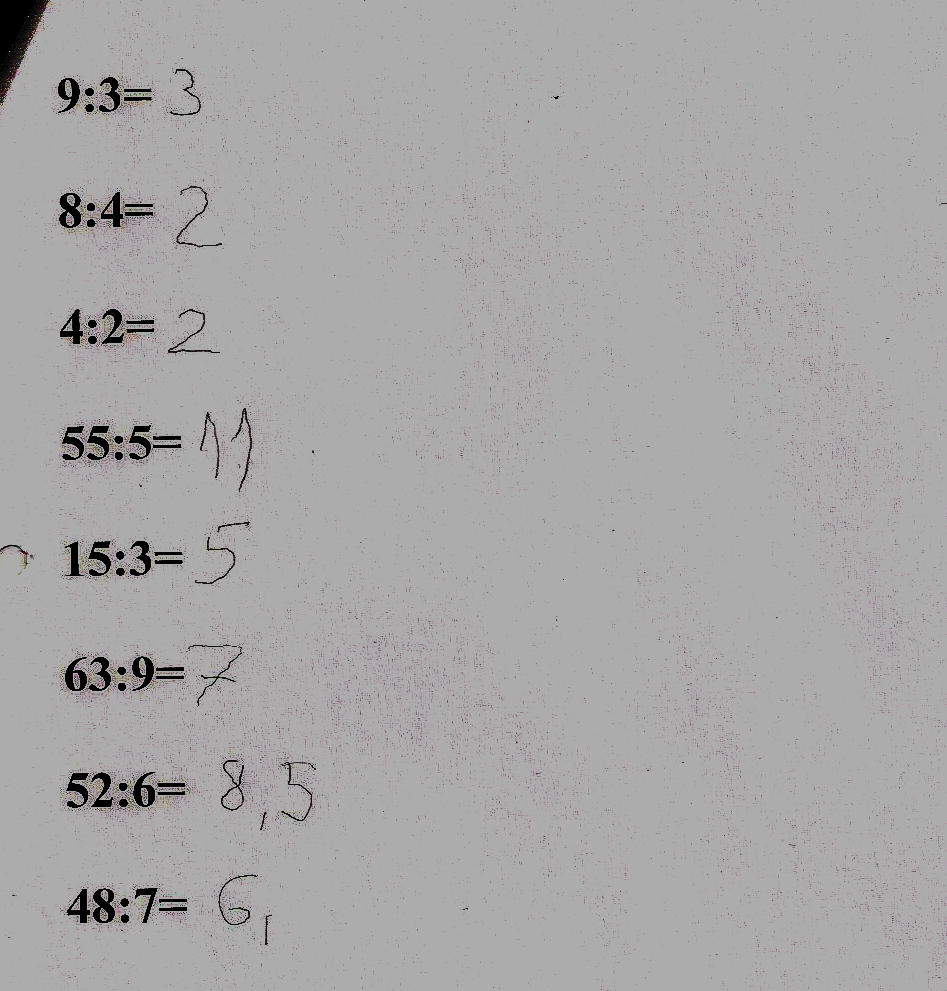

TÖRTSZÁMOK KÖZÖS NEVEZŐRE SZORZÁSA ÉS ÖSSZEADÁSA
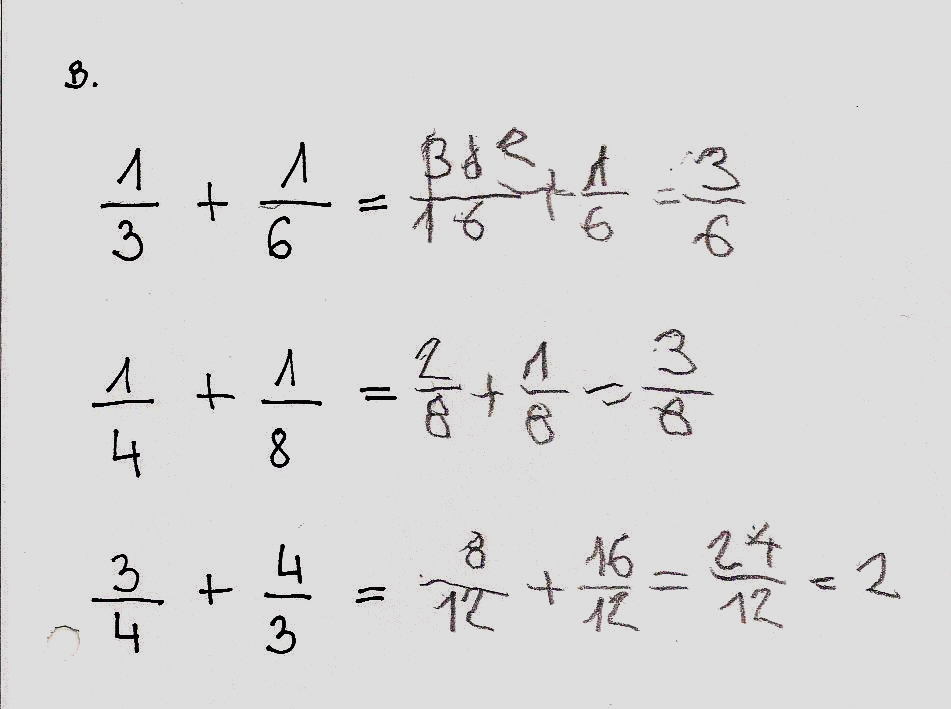
„MEGFORDÍTOTT” MŰVELETEK
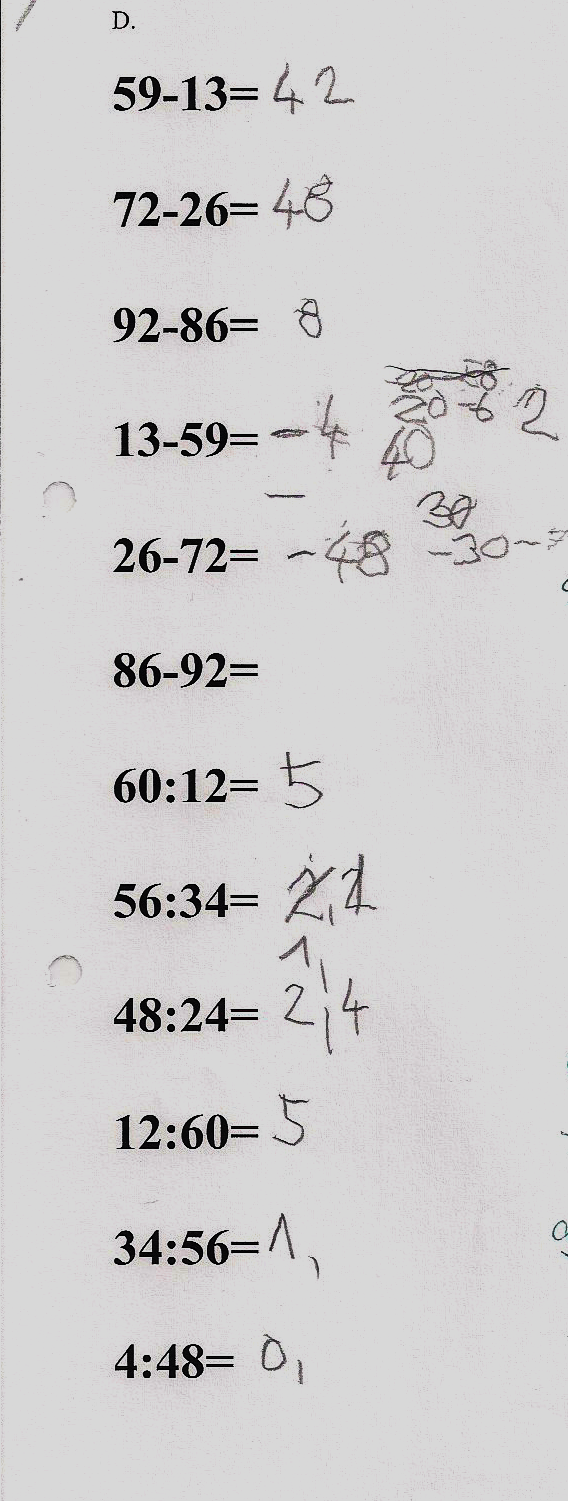
EGYSZERES ZÁRÓJELEKKEL VÉGZETT MŰVELETEK


KÉTSZERES ZÁRÓJELEK MELLETTI MŰVELETEK
ZÁRÓJELES KONSTRUKCIÓK GENERÁLÁSA

SZÁMOK REKURZÍV SOROZATÁNAK GENERÁLÁSA

NORMÁL KONTROLL: PÉLDÁK
ZÁRÓJELES KONSTRUKCIÓK GENERÁLÁSA

NORMÁL KONTROLL: PÉLDÁK
SZÁMOK REKURZÍV SOROZATÁNAK GENERÁLÁSA

Köszönettel tartozunk Kotra Mónikának, Örley Zitának és Zsitvai Mihálynak a tesztelések során végzett munkájukért.↩
Az afáziás személy nyelvi produkciós és megértési képességeit a WAB (Western Aphasia Battery)
szűrőteszttel (magyarra adaptált változata: Osmánné, Sági 1991) illetve a Token beszédértést vizsgáló teszttel
(magyar adaptáció: Osmánné, Sági 1994) mértük fel. A WAB teszt szubtesztekből áll, ezek a beszéd
folyékonyságát, információtartalmát, a megértést, az ismétlést és a megnevezést értékelő, egytől tízig pontozó
szubtesztek. A szubtesztbeli pontok összegének kétszerese adja az Afázia Együtthatónak (AQ) nevezett értéket.
Ép nyelvhasználatról akkor beszélnek, ha az elért összpontszám : 93.8 vagy afeletti. A pontok értékeinek
megoszlása mentén a szűrőteszt nyolcféle kategóriába sorolja a személyeket: globális, izolációs, Broca,
transzkortikális motoros, Wernicke, transzkortikális szenzoros, vezetéses és anómikus afáziások. Hangsúlyozni
kell, hogy ezek kifejezetten a nyelvi szűrőteszt kategóriái. Például a Broca afázia kategóriát akkor adja a teszt, ha
a fluencia a 0-4 közötti pontértékek, a megértés a 4-10, az ismétlés 8-nál alacsonyabb, a megnevezési teljesítmény
pedig pedig a 0-8 értékek közé esik. A vezetéses és az anómikus afázia kategóriáját akkor adja a teszt, ha a
fluencia pontértékek egyaránt 5-10 közti, a megértés egyaránt 7-10 pontértékek közé esik, viszont a szó- és
mondatismétlési teljesítmény a vezetéses afáziánál: a 0 -6.9, míg az anómikus afáziánál a 7-10 pontértékek közé
esik, a megnevezésnél pedig egyaránt 0-9 közötti pontértékek vannak. A Token komplex beszédmegértési tesztben
pedig a maximális eredmény: 36.↩
A számtani műveleteknek létezik egy alapsorrendje: miszerint, ha összeadás és kivonás következik egymás
után, akkor a sorrend tetszőleges. Az osztás illetve szorzás és a kivonás illetve összeadás esetében az osztás illetve a szorzás az elsődleges. Az osztás és a szorzás között zárójellel kell a sorrendet jelezni: (6 : 3) × 2 = 4, 6 : (3 × 2)
=1. Bonyolultabb kifejezéseknél először a zárójelben levő kifejezéseket számoljuk ki, a zárójelen belül pedig a szorzás és az osztás elsőbbséget élvez a kivonásához vagy összeadáshoz képest. Például: 3 × (20 - 5 × 2) = 3 × (20 - 10) = 3 × 10 = 30. A szorzás, illetve az osztás, valamint az összeadás és kivonás elvégzésének a sorrendje a zárójelezéssel módosítható: (6 + 2) × 5 + 8 = 48; 6 + (2 × 5) + 8 = 24; 6 + 2 × (5 + 8) = 32.↩