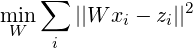
We analyze whether different sense vectors of the same word form in multi-sense word embeddings correspond to different concepts. On the more technical side of embedding-based dictionary induction, we also test whether the orthogonality constraint and related vector preprocessing techniques help in reverse nearest neighbor search. Both questions receive a negative answer.
Word sense induction (WSI) is the task of discovering senses of words without supervision (Schütze, 1998). Recent approaches include multi-sense word embeddings (MSEs), i.e. vector space models of word distribution with more vectors for ambiguous words. In MSEs, each vector is supposed to correspond to a different word sense, but in practice models frequently have different sense vectors for the same word form without an interpretable difference in meaning.
In Borbély et al. (2016), we proposed a cross-lingual method for the evaluation of sense resolution in MSEs. The method is based on the principle that words may be ambiguous to the extent to which their postulated senses translate to different words in some other language. For the translation of words, we applied the method by Mikolov et al. (2013b) who train a translation mapping from the source language embedding to the target as a least-squares regression supervised by a seed dictionary of the few thousand most frequent words. The translation of a source word vector is the nearest neighbor of its image by the mapping in the target space. In the multi-sense setting, we have translated from MSEs. (The target embedding remained single-sense.)
Section 1 discusses our linguistic motivation; and Section 2 introduces MSEs. In Section 3, we elaborate on the cross-lingual evaluation. Part of the evaluation task is to decide on empirical grounds whether different good translations of a word are synonyms or translations in different senses. Reverse nearest neighbor search, the orthogonality constraint on the translation mapping, and related techniques are also discussed. Section 4 offers experimental results with quantitative and qualitative analysis. It should be noted that our evaluation is not very strict, but rather a process of looking for something conceptually meaningful in present-day unsupervised MSE models.1
We emphasize that our evaluation proposal probes
an aspect of MSEs,
The goal of WSI can be set at two levels. We may more modestly aim to distinguish homophony from polysemy. Ideally, we could even differentiate between metonymy and metaphor, two subtypes of polysemy, discussed in more detail by Veronika Lipp in the next section.
Lexical ambiguity is linguistically subdivided into
two main categories:
Two criteria have been proposed for the distinction
between homonymy and polysemy. The first criterion
has to do with the
The second criterion for the distinction between
homonymy and polysemy has to do with the
Most discussions about lexical ambiguity, within
theoretical and computational linguistics, concentrate
on polysemy, which can be further divided into two
types (Apresjan, 1974; Pustejovsky, 1995). The first
type of polysemy is motivated by
Vector-space language models with more vectors for
each meaning of a word originate from Reisinger and
Mooney (2010). Huang et al. (2012) trained the first
neural-network-based MSE. Both works use a
uniform number of clusters for all words that they
select before training as potentially ambiguous.
The first system with adaptive sense numbers and
an effective open-source implementation is a
modification of skip-gram Mikolov et al. (2013c),
Bartunov et al. (2016) and Li and Jurafsky (2015)
improve upon the heuristic thresholding by
formulating text generation as a Dirichlet process. In
MSEs are still in the research phase: Li and Jurafsky (2015) demonstrate that, when meta-parameters are carefully controlled for, MSEs introduce a slight performance boost in semantics-related tasks (semantic similarity for words and sentences, semantic relation identification, part-of-speech tagging), but similar improvements can also be achieved by simply increasing the dimension of a single-sense embedding.
Mikolov et al. (2013b) discovered that embeddings of different languages are so similar that a linear transformation can map vectors of the source language words to the vectors of their translations.
The method uses a seed dictionary of a few thousand
words to learn translation as a linear mapping
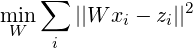
and can be used to collect translations for the whole
vocabulary by choosing
In a multi-sense embedding scenario, Borbély et al. (2016) take an MSE as the source model, and a single-sense embedding as target. The quality of the translation has been measured by training on the most frequent 5k word pairs and evaluating on another 1k seed pairs.
A common problem when looking for nearest
neighbors in high-dimensional spaces (Radovanović
et al., 2010; Suzuki et al., 2013; Tomašev and
Mladenic, 2013), and especially in embedding-based
dictionary induction (Dinu et al., 2015; Lazaridou
et al., 2015) is when there are
In reverse NN search, we restricted the vocabulary
to the some tens of thousands of the most frequent
words. We introduced this restriction for memory
saving, because the
Xing et al. (2015) note that the original linear
translation method is theoretically inconsistent due
to its being based on three different similarity
measures:
among the mapped points
We trained
We implemented the orthogonal restriction by computing the singular value decomposition
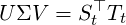
where
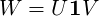
where
| 8192 | 16384 | 32768 | |||||||||||
| general linear | orthogonal | general linear | orthogonal | general linear | orthogonal
| ||||||||
| any | disamb | any | disamb | any | disamb | any | disamb | any | disamb | any | disamb | ||
fwd | vanilla | 28.7% | 2.40% | 32.1% | 2.40% | 36.2% | 3.40% | 42.0% | 4.70% | 36.7% | 4.20% | 44.5% | 6.00% |
| normalize | 28.2% | 2.20% | 3.40% | 35.1% | 2.80% | 5.80% | 36.6% | 3.80% | 6.00% | ||||
| + center | 26.6% | 2.10% | 32.8% | 2.90% | 32.9% | 2.70% | 42.0% | 4.50% | 34.6% | 3.50% | 43.9% | 5.50% | |
rev | vanilla | 11.85% | 51.7% | 11.37% | 11.99% | 56.6% | 12.59% | 23.60% | 73.6% | 22.30% | |||
| normalize | 53.3% | 11.61% | 50.0% | 10.90% | 58.0% | 12.35% | 56.5% | 12.59% | 73.7% | 24.20% | 72.8% | 22.10% | |
| + center | 51.7% | 11.37% | 53.3% | 11.14% | 57.1% | 11.99% | 57.7% | 12.35% | 69.7% | 22.20% | 73.5% | 23.00% | |
Table 1 shows the effect of these factors. Precision in forward NN search follows a similar trend to that in Xing et al. (2015) and Artetxe (2016): the best combination is an orthogonal mapping between length-normalized vectors; however, centering did not help in our experiments. Reverse NNs yield much better results than the simpler method, but none of the orthogonality-related techniques give further improvement here. The cause of reverse NN’s apparent insensitivity to length may be the topic of further research.
We evaluate MSE models in two ways, referred to as
| | | |||||
| | | |||||
| | ||||||
| | |
|||||
| | |
|||||
| | | |
||||
| | |
|||||
| | |
|||||
| | | |
||||
| | |
|||||
In
| covg | ||||
| E | -0.04849 | függő | addict, aerial | 0.4 |
| S | 0.01821 | alkotó | constituent, creator | 0.5 |
| S | 0.05096 | előzetes | preliminary, trailer | 1.0 |
| S | 0.0974 | kapcsolat | affair, conjunction, linkage | 0.33 |
| I | 0.1361 | kocsi | coach, carriage | 1.0 |
| S | 0.136 | futó | runner, bishop | 1.0 |
| S | 0.1518 | keresés | quest, scan | 0.67 |
| S | 0.1574 | látvány | outlook, scenery, prospect | 0.6 |
| S | 0.1626 | fogad | bet, greet | 1.0 |
| S | 0.1873 | induló | march, candidate | 1.0 |
| I | 0.187 | nemes | noble, peer | 0.67 |
| E | 0.1934 | eltérés | variance, departure | 0.4 |
| E | 0.1943 | alkalmazás | employ, adaptation | 0.33 |
| S | 0.2016 | szünet | interval, cease, recess | 0.43 |
| E | 0.2032 | kezdeményezés | initiation, initiative | 1.0 |
| S | 0.2052 | zavar | disturbance, annoy, disturb, turmoil | 0.57 |
| S | 0.2054 | megelőző | preceding, preventive | 0.29 |
| IE | 0.2169 | csomó | knot | 1.0 |
| E8 | 0.21 | remény | outlook, promise, expectancy | 0.6 |
| S | 0.2206 | bemutató | exhibition, presenter | 0.67 |
| E | 0.2208 | egyeztetés | reconciliation, correlation | 0.5 |
| S | 0.237 | előadó | auditorium, lecturer | 0.67 |
| E | 0.2447 | nyilatkozat | profession, declaration | 0.4 |
| I | 0.2494 | gazda | farmer, boss | 0.67 |
| I | 0.2506 | kapu | gate, portal | 1.0 |
| I | 0.2515 | előbbi | anterior, preceding | 0.67 |
| I | 0.2558 | kötelezettség | engagement, obligation | 0.67 |
| E | 0.265 | hangulat | morale, humour | 0.5 |
| E | 0.2733 | követ | succeed, haunt | 0.67 |
| SE | 0.276 | minta | norm | 0.75 |
| S | 0.2807 | sorozat | suite, serial, succession | 1.0 |
| S | 0.2935 | durva | coarse, gross | 0.18 |
| I | 0.3038 | köt | bind, tie | 0.67 |
| E | 0.3045 | egyezmény | treaty, protocol | 0.67 |
| I | 0.3097 | megkülönböztetés | discrimination, differentiation | 0.5 |
| I | 0.309 | ered | stem, originate | 0.5 |
| I | 0.319 | hirdet | advertise, proclaim | 1.0 |
| E | 0.3212 | tartós | substantial, durable | 1.0 |
| I | 0.3218 | ajánlattevő | bidder, supplier, contractor | 0.6 |
| I | 0.3299 | aláírás | signing, signature | 0.67 |
| I | 0.333 | bír | bear, possess | 1.0 |
| I | 0.3432 | áldozat | sacrifice, victim, casualty | 1.0 |
| IE | 0.3486 | kerület | ward | 0.3 |
| I | 0.3486 | utas | fare, passenger | 1.0 |
| I | 0.3564 | szigorú | stern, strict | 0.5 |
| I | 0.3589 | bűnös | sinful, guilty | 0.5 |
| I | 0.3708 | rendes | orderly, ordinary | 0.5 |
| I | 0.3824 | eladó | salesman, vendor | 0.5 |
| I | 0.3861 | enyhe | tender, mild, slight | 0.6 |
| I | 0.3897 | maradék | residue, remainder | 0.33 |
| I | 0.3986 | darab | chunk, fragment | 0.4 |
| E | 0.4012 | hiány | poverty, shortage | 0.5 |
| I | 0.4093 | kutatás | exploration, quest | 0.5 |
| I | 0.4138 | tanítás | tuition, lesson | 0.67 |
| I | 0.4196 | őszinte | frank, sincere | 0.67 |
| I | 0.4229 | környék | neighborhood, surroundings, vicinity | 0.38 |
| I | 0.4446 | ítélet | judgement, sentence | 0.67 |
| I | 0.4501 | gyerek | childish, kid | 0.67 |
| I | 0.4521 | csatorna | ditch, sewer | 0.4 |
| I | 0.4547 | felügyelet | surveillance, inspection, supervision | 0.43 |
| E | 0.4551 | ritka | rare, odd | 0.5 |
| S | 0.4563 | szerető | fond, lover, affectionate, mistress | 0.67 |
| I | 0.4608 | szeretet | affection, liking | 0.67 |
| I | 0.4723 | vizsgálat | inquiry, examination | 0.67 |
| I | 0.4853 | tömeg | mob, crowd | 0.5 |
| I | 0.4903 | puszta | pure, plain | 0.22 |
| I | 0.4904 | srác | kid, lad | 1.0 |
| I | 0.4911 | büntetés | penalty, sentence | 0.29 |
| I | 0.4971 | képviselő | delegate, representative | 0.67 |
| I | 0.4975 | határ | boundary, border | 0.67 |
| I | 0.5001 | drága | precious, dear, expensive | 1.0 |
| S | 0.5093 | uralkodó | prince, ruler, sovereign | 0.5 |
| I | 0.5097 | válás | separation, divorce | 0.67 |
| I | 0.5103 | ügyvéd | lawyer, advocate | 0.67 |
| I | 0.5167 | előnyös | advantageous, profitable, favourable | 1.0 |
| I | 0.5169 | merev | rigid, strict | 1.0 |
| I | 0.5204 | nyíltan | openly, outright | 1.0 |
| I | 0.5217 | noha | notwithstanding, albeit | 1.0 |
| I | 0.5311 | hulladék | litter, garbage, rubbish | 0.43 |
| I | 0.5311 | szemét | litter, garbage, rubbish | 0.43 |
| I | 0.5612 | kielégítő | satisfying, satisfactory | 1.0 |
| E | 0.5617 | vicc | joke, humour | 1.0 |
| I | 0.5737 | szállító | supplier, vendor | 1.0 |
| I | 0.5747 | óvoda | nursery, daycare, kindergarten | 1.0 |
| I | 0.5754 | hétköznapi | mundane, everyday, ordinary | 0.75 |
| I | 0.5797 | anya | mum, mummy | 1.0 |
| I | 0.5824 | szomszédos | neighbouring, neighbour | 0.4 |
| E | 0.5931 | szabadság | liberty, independence | 1.0 |
| I | 0.6086 | lelkész | pastor, priest | 0.4 |
| I | 0.6304 | fogalom | notion, conception | 1.0 |
| I | 0.6474 | fizetés | salary, wage | 0.67 |
| I | 0.6551 | táj | landscape, scenery | 1.0 |
| I | 0.6583 | okos | clever, smart | 0.67 |
| I | 0.6707 | autópálya | highway, motorway | 0.5 |
| I | 0.6722 | tilos | prohibited, forbidden | 1.0 |
| I | 0.6811 | bevezető | introduction, introductory | 1.0 |
| I | 0.7025 | szövetség | coalition, alliance, union | 0.75 |
| I | 0.7065 | fáradt | exhausted, tired, weary | 1.0 |
| I | 0.7066 | kiállítás | exhibit, exhibition | 0.67 |
| I | 0.7135 | hirdetés | advert, advertisement | 1.0 |
| I | 0.7147 | ésszerű | rational, logical | 1.0 |
| I | 0.7664 | logikai | logic, logical | 1.0 |
| I | 0.7757 | szervez | organise, organize, arrange | 1.0 |
| I | 0.8122 | furcsa | strange, odd | 0.4 |
| I | 0.8277 | azután | afterwards, afterward | 0.67 |
| I | 0.8689 | megbízható | dependable, reliable | 0.67 |
Table 3 shows the successfully disambiguated
words sorted by the cosine similarity
We see that most words with
The clearest case of homonymy is when unrelated
senses belong to different parts of speech
(POSs), and the translations reflect these
POSs, e.g.
More interesting are word forms with related senses
in the same POS, e.g.
1957 was an influential year in linguistics:
Harris (1957) developed the frequency-aware variant of the distributional method, Osgood et al. (1957)
pioneered vector space models, and the author of a
more recent conceptual meaning representation
framework (Kornai, 2010, in press) was born. Fifty
years later (more precisely in fall 2006) I met András
during a class he taught on the book he was writing
(Kornai, 2007). I heard about
Laozi says that a good leader does not leave a footprint, and András encouraged us to be independent and effective. One of his remarkable citations is that “It’s easier to ask forgiveness than it is to get permission”. The proverb is sometimes attributed to the Jesuits, who are similar to András in having had a great impact on what I’ve become in the past ten years. The real source of the proverb is Grace Hopper, a US navy admiral who invented the first compiler. This paper is a step in my learning to be so effective as the sources mentioned above.
András Kornai, besides the work already acknowledged, rated each item in Table 3. I would like to thank the anonymous reviewer for detailed critique, both substantial and linguistic, Mátyás Lagos for reviewing language errors, and Gábor Recski and Bálint Sass for their useful comments. The orthogonal approximation was implemented following a code10 by Gábor Borbély.
Judit Ács, Katalin
Pajkossy, and András Kornai. 2013. Building
basic vocabulary across 40 languages. In
Ju. D. Apresjan. 1974. Regular polysemy.
Mikel Artetxe, Gorka Labaka, and Eneko
Agirre. 2016. Learning principled bilingual
mappings of word embeddings while preserving
monolingual invariance. In
Sergey Bartunov, Dmitry Kondrashkin, Anton
Osokin, and Dmitry Vetrov. 2016. Breaking
sticks and ambiguities with adaptive skip-gram.
In
Gábor Borbély, Márton Makrai, Dávid Márk
Nemeskey, and András Kornai.
2016. Evaluating multi-sense embeddings for
semantic resolution monolingually and in word
translation. In
Alan D. Cruse. 2004.
Georgiana Dinu, Angeliki Lazaridou, and
Marco Baroni. 2015. Improving zero-shot
learning by mitigating the hubness problem. In
Manaal Faruqui and Chris Dyer. 2014.
Improving vector space word representations
using multilingual correlation. In
Péter Halácsy, András Kornai,
László Németh, András Rung, István Szakadát,
and Viktor Trón. 2004. Creating open language
resources for Hungarian. In
Zellig Harris. 1957. Coocurence and
transformation in liguistic structure.
Eric Huang, Richard Socher, Christopher
Manning, and Andrew Ng. 2012. Improving
word representations via global context and
multiple word prototypes. In
R. Jackendoff. 2002.
András Kornai. 2007.
András Kornai. 2010. The algebra of lexical
semantics. In Christian Ebert, Gerhard Jäger,
and Jens Michaelis, editors,
András Kornai. in press.
András Kornai, Judit Ács, Márton Makrai,
Dávid Márk Nemeskey, Katalin Pajkossy, and
Gábor Recski. 2015. Competence in lexical
semantics. In
Angeliki Lazaridou, Georgiana Dinu, and
Marco Baroni. 2015. Hubness and pollution:
Delving into cross-space mapping for zero-shot
learning. In
Jiwei Li and Dan
Jurafsky. 2015. Do multi-sense embeddings
improve natural language understanding? In
John Lyons. 1977.
Tomas Mikolov, Kai Chen, Greg Corrado,
and Jeffrey Dean. 2013a. Efficient estimation
of word representations in vector space. In
Y. Bengio and Y. LeCun, editors,
Tomas Mikolov, Quoc V Le, and Ilya Sutskever. 2013b. Exploiting similarities among languages for machine translation. Xiv preprint arXiv:1309.4168.
Tomas Mikolov, Ilya Sutskever, Kai Chen,
Greg S
Corrado, and Jeff Dean. 2013c. Distributed
representations of words and phrases and
their compositionality. In C.J.C. Burges,
L. Bottou, M. Welling, Z. Ghahramani, and
K.Q. Weinberger, editors,
Tomas Mikolov, Wen-tau Yih, and Geoffrey
Zweig. 2013d. Linguistic regularities in
continuous space word representations. In
Gregory Murphy. 2002.
Arvind Neelakantan,
Jeevan Shankar, Alexandre Passos, and Andrew
McCallum. 2014. Efficient non-parametric
estimation of multiple embeddings per word in
vector space. In
Csaba Oravecz, Tamás Váradi, and Bálint
Sass. 2014. The Hungarian Gigaword Corpus.
In
Charles E. Osgood, George Suci, and Percy
Tannenbaum. 1957.
Jeffrey Pennington, Richard Socher, and
Christopher Manning. 2014. Glove: Global
vectors for word representation. In
James Pustejovsky. 1995.
M Radovanović, A Nanopoulos,
and M Ivanović. 2010. Hubs in space:
Popular nearest neighbors in high-dimensional
data.
Joseph Reisinger and Raymond J Mooney.
2010. Multi-prototype vector-space models
of word meaning. In
Hinrich Schütze. 1998. Automatic word sense
discrimination.
I Suzuki, K Hara, M Shimbo, M Saerens,
and K Fukumizu. 2013. Centering similarity
measures to reduce hubs. In
N Tomašev and D Mladenic. 2013. Hub
co-occurrence modeling
for robust high-dimensional knn classification.
In
Chao Xing, Chao Liu, Dong Wang, and
Yiye Lin. 2015. Normalized word embedding
and orthogonal transform for bilingual word
translation. In