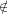 Q; Q
natural iff either Q is positive and E ∈ Q or Q is not positive and E
Q; Q
natural iff either Q is positive and E ∈ Q or Q is not positive and E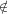 Q. Two natural
quantifiers have the same polarity iff either both are positive or neither of them is
positive.
Q. Two natural
quantifiers have the same polarity iff either both are positive or neither of them is
positive.
Abstract
Raised verb phrases denote elements of ℘(℘(℘(E))), that is sets of type ⟨1⟩ quantifiers (and not just sets). Various arguments supporting the necessity of the VP raising, similar to the noun phrase raising, are given. Most of the presented arguments are related to the semantics of the higher order comparative the same and the semantics of the reciprocal each other but some other constructions with raised VPs are also discussed. Predicates formed by such constructions are ”non-homomorphic” because they denote sets of quantifiers whose characteristic functions are not homomorphisms (from the algebra of quantifiers to the algebra of truth-values). Some formal properties and analogies with ”classically” raised NPs are indicated.
The results of combinatorial logic allow us to abandon, in certain cases, the distinction
between an argument and the function of which it is the argument: informally, the
argument of a function can become the function having as argument the function
of which it was the argument. More formally, in the categorial grammar which
includes ”functional categories” and where grammatical categories are associated
with logical types, an expression can be associated with at least two types: if
it occurs ”initially” in type a it may also occur in any type ⟨⟨a,b⟩,b⟩ for any
type b. Probably having this in mind, Montague made his by now well-known
move which led to the uniform treatment of noun phrases which all, including
proper nouns, denote sets of properties. Using the elementary notion from the
categorial grammar in which NP and S are primitive categories, and ignoring the
directionality, Montague’s idea restricted to these particular categories, can be
illustrated, at the syntactic level, by the fact that sequences of categories in (1) and (2)
reduce, via the function application (symbolised by ”+”), to the same category
S:
(1) NP + S∕NP=S
(2) S∕(S∕NP) + S∕NP=S
At the semantic level adding (2) to the grammar amounts to considering that denotations of proper nouns, which ”classically” denote individual objects, that is objects of type e, get a ”new” denotation which is the ultrafilter generated by the element of the model corresponding to the referent of the proper noun and is now of type ⟨⟨e,t⟩,t⟩. This move makes it easy in particular to compute the semantic values of Boolean compounds of proper nouns with other NPs since in this case Boolean connectors are interpreted by the corresponding Boolean operations.
In (1) the first element is considered as an argument expression and the second as the functional expression. In (2) the roles are inverted: the first element is the functional expression and the second- the argument expression. Thus in (2) a type-raising rule, generally admitted in categorial grammars has been applied: this rule turns arguments into functions over functions over these arguments.
Type-raising is one of the tools used in the strategy of flexible categories that is the proposal that some linguistic units identified by the (categorial) grammar may have many categories associated with them and thus take their denotations among various logical types. As seen from (1) and (2) type-raising is related to the rule of function application. Other syntactic rules, such as for instance function composition (cf. Geach 1972), can be used to define other type changing operators which enrich the tools allowing type shifting (cf. Partee and Rooth 1983, Partee 1987 for some empirically justified pioneering proposals).
Obviously from a theoretical point of view there is no reason for this process of inversion
of roles between a function and its argument to stop: the reduction indicated in (3) is also
possible:
(3) S∕(S∕NP)+ S(S∕(S∕NP)) = S
In (2) the category of the subject NP has been raised to the functional category
S(S∕NP)) and in (3) the verb phrase which was the argument expression of category
S∕NP in (2) becomes functional expression of category S(S∕(S∕NP)). Thus in (3) the V P
has been raised to the category S(S∕(S∕NP)) whose type is now ⟨⟨⟨e,t⟩t⟩t⟩. This means
that such raised VPs denote a set of type ⟨1⟩ quantifiers and consequently the sentence of
the form (4), where V PR is a raised V P (that is V PR is the abbreviation of the category
S(S∕(S∕NP))), is true iff the quantifier denoted by the NP belongs to the set denoted by
the V PR:
(4) NP + V PR
Of course V PR is a verb phrase. It gets an additional category, that is V PR is an abbreviation of S(S∕(S∕NP)) and is interpreted now by objects of type ⟨⟨⟨e,t⟩t⟩t⟩ that is it denotes elements of ℘(℘(℘(E))). Consequently, given this alternative, verb phrases act as functions taking subject NPs (which in this case necessarily denote type ⟨⟨e,t⟩,t⟩ objects) as arguments.
In this article I give some empirical reasons in favour of adding a rule like the one in (3) to the grammar. In other words, I will indicate a series of linguistic data which can be uniformly treated in the framework in which it is assumed that in addition to the subject NPs also verb phrases have to be raised. To do this I will discuss the semantics of some specific linguistic constructions which induce or force the raising of VPs to which they are related. Consequently, at the semantic level, I will show that it is useful, if not necessary, to suppose that in some cases verb phrases denote sets of type ⟨1⟩ quantifiers.
The idea of type shifting is that the type of some categories can change depending on the environment they find themselves in. This means that the type of a given category has to be changed only in some grammatical constructions. A consequence of this is the fact that lifted VPs are not morphologically or syntactically ”simple” since they are usually results of various operations due to lift inducers, sometimes language specific. Probably for this reason the proposal that languages might differ from each other by cases in which it is the subject NP or the VP which takes the other as argument is not new. In addition some specific linguistic phenomena may be better treated in such an extended framework. For instance Bach (1980) relates the difference between tensed and untensed intransitive VPs precisely to the difference in types associated with them. Similarly, it has been occasionally suggested that the specific ”plural verbs” such as to gather or collective predicates have their type raised and thus that they denote (such as meet denote elements of ℘(℘(E)) (Van der Does 1993). However, as far as I know, this VP raising always goes in pair with type shifting of nominal elements, in particular of determiners, as well. For Van der Does (1993) the ordinary determiners which ”classically” are relations between sets, get an additional type making them relations between sets and sets of sets.
A special case of VPs with higher type is discussed in Partee and Rooth (1983). This case is special since it involves intensionality explicitly: in order to account for the semantics of complex VP which are conjunctions of intensional with extensional verbs such complex VPs have to get the raised, higher order type.
More generally, Keenan and Faltz (1985) propose that (extensional) VPs always denote specific characteristic functions of a set of type ⟨1⟩ quantifiers, that is they denote a set of quantifiers. Given that these characteristic functions are in addition homomorphisms (from the algebra of quantifiers to the algebra of truth-values) they indicate that the denotational domain of VPs that they propose is isomorphic to the algebra of sets (subsets of the universe), the classical denotational domain of one-place predicates in the first order logic. At the same time Keenan and Faltz (1985, p. 265) indicate that in natural languages there exist various ”non-homomorphic” predicates such as for instance collective and reciprocal predicates, which cannot denote in the denotational domain of VPs that they propose.
In this paper I argue for the change in the denotational type of VPs. I will mainly discuss complex verb phrases containing transitive verbs whose second argument, the argument in the object position, is what I will call a generalised noun phrase (GNP), that is an expression which can play the role of nominal arguments of a verb, as does an ordinary NP, but which cannot freely occur in all argumental positions of the verb (cf. Zuber, forthcoming). These expressions will be characterised by their logical properties and not by their syntactic properties. A typical example of such a GNP is the reciprocal each other and various Boolean compounds of it with ordinary NPs or reflexive NPs. Another example which will be discussed at some length is given by the ”higher order” comparative like the same CN or the same number of CN. It will be indicated that such GNPs, which force the raising of VPs, have various logical properties which differentiate them from ordinary NPs in the object position.
The second series of constructions I will discuss concerns raised VPs formed from intransitive VPs. Such VPs, whose semantics necessitates raising can be either simple intransitive VPs or complex VPs with the intransitive verb modified by specific adverbials or gerundives which induce the raising. As we will see, such adverbials are usually semantically related to GNPs. In this context I will mention a possible analysis of cumulative readings of some quantifiers and some other readings related to the plurality of subject NPs, in which the rule of VPs raising is explicitly used. In fact it will appear that cumulative readings (of NPs in subject and object positions) can be, or even should be, related to the semantics of the GNPs such as the same or each other. More generally, it will appear that many expressions forcing the raising of VPs are semantically related and some of them, roughly speaking, are defined by others, at least at up to some ”degree of equivalence”.
Finally, I will recall that, as it is the case with proper nouns when they occur in conjunction with quantified NPs, ”Booleanly” simple VPs, given by intransitive verbs, and which are of type ⟨e,t⟩, must have their type raised when they occur in conjunctions with (simple or complex) VPs whose type is raised. Some other similarities with the NP raising will be indicated and in particular the existence of the inverse rule of VP lowering. For this reason we will call VP raising classical raising.
To conclude these introductory remarks I want to stress that the purpose of this paper is not to give a full or detailed semantics of the constructions which will be mentioned. I will discuss essentially examples of syntactically complex constructions whose semantics has already been specified precisely in the spirit of the proposal made in this article. Indeed, it seems obvious that VPs may non-trivially denote types other than that of sets only when they form syntactically complex constructions.
We will consider binary relations and functions, in particular type ⟨1⟩ quantifiers, over a universe E. To note the type of function we will use not only Montagovian notation. In particular the type of functions from binary relations to sets of type ⟨1⟩ quantifiers will be noted ⟨2 : ⟨1⟩⟩ and the type of functions having binary relations and sets as arguments and sets of type ⟨1⟩ quantifiers as output will be noted ⟨2,1 : ⟨1⟩⟩.
If R is a binary relation, D(R) denotes its domain.The relation I is the identity relation: I = {⟨x,y⟩ : x = y}. If R is a binary relation and X a set then R∕X = R ∩ (X × X). The binary relation RS is the greatest symmetric relation included in R, that is RS = R ∩R−1 and RS− = RS ∩ I′ is the greatest symmetric irreflexive relation included in R. For any binary relation R and any set A, the relation RA is the subset of R defined as RA = {⟨x,y⟩ : ⟨x,y⟩∈ R ∧ y ∈ A}.
Let Q be a type ⟨1⟩ quantifier. Q is atomic iff it is a singleton. An atomic quantifier
containing A as its only element will be noted QA. Q is positive, Q ∈ POS iff ∅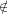 Q; Q
natural iff either Q is positive and E ∈ Q or Q is not positive and E
Q; Q
natural iff either Q is positive and E ∈ Q or Q is not positive and E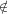 Q. Two natural
quantifiers have the same polarity iff either both are positive or neither of them is
positive.
Q. Two natural
quantifiers have the same polarity iff either both are positive or neither of them is
positive.
We will also use the property living on displayed by type ⟨1⟩ quantifiers (cf. Barwise and Cooper 1981). The type ⟨1⟩ quantifier Q lives on a set A (where A ⊆ E) iff for all X ⊆ E, Q(X) = Q(X ∩ A). If E is finite then there is always a smallest set on which a quantifier Q lives. The fact that A is a set on which Q lives will be noted Li(Q,A) and the fact that A is a smallest set on which Q lives will be noted SLi(Q,A). If Li(Q,A) and B ⊆ A ∧ B ∈ Q then B is a witness set of Q. The fact that B is a witness set of the quantifier Q, which lives on A, will be noted B = Wt(Q,A). If Li(Q,A) then A ∈ Q iff E ∈ Q and thus if E ∈ Q and Li(Q,A) then A = Wt(Q,A).
Observe that any principal filter is a positive type ⟨1⟩ quantifier which lives on the set by which it is generated, and, moreover this set is its witness set. Atomic quantifiers live on the universe E only.
Concerning syntactic aspects we will use a ”simple extended categorial grammar” admitting flexible categories. Thus we assume that for each derived category C of the form C = A∕B there is a rule stating that an expression of category A can be built by combining an expression of category B with an expression of category C. For any grammatical category C there is a corresponding denotational Boolean algebra DC of possible denotations of expressions of category C. Expressions of the derived category A∕B take their denotations in the algebra DA∕B which is the algebra of functions from DB to DA. Furthermore, given that most categories are functionally related (in principle all ”major” categories are Boolean), the corresponding denotational algebras are not independent of each other. In particular the elements of the algebra DA∕B are functions from DB to DA. Given that functions interpreting functional expressions in general satisfy various constraints, one usually considers just some sub-algebras of the algebra of all functions from DB to DA. For instance NPs denote in the algebra DS∕V P of type ⟨1⟩ quantifiers.
Among type ⟨1⟩ quantifiers we distinguish nominal individuals Ia defined as Ia = {Y : Y ⊆ E ∧a ∈ Y }. Nominal individuals are denotations of proper nouns. They are obtained precisely by the operation of type raising applied to (denotations of) proper nouns ”initially” having as denotation objects of type e. Nominal individuals belong to the class of quantifiers called principal filters generated by a set. Thus Ft(A), the (principal) filter generated by the set A (for A ⊆ E), is defined as: Ft(A) = {Y : Y ⊆ E ∧ A ⊆ Y }.
The notion of an individual can in fact be associated with any Boolean denotational
algebra:
D1: Let B be an atomic Boolean algebra and I ⊆ B. Then I is an individual on B iff
χI, the characteristic function of I, is a homomorphism from B to the algebra
{0,1}
Nominal individuals are individuals on the algebra of sets in the sense of D1.
An individual I on B is generated by the atom α of B iff α ≤ i for any i ∈ I. Individuals
of an atomic algebra B, generated by an atom of B, thus defined are exactly the sets of
elements of B which satisfy (1) the meet, (2) the join and (3) the complement conditions.
More formally, if I is an individual (on the algebra B, generated by an atom of B) then for
any S ⊆ B, we have (1) S ⊆ I iff ∧
S ∈ I, (2) S ∩I≠∅ iff ∨
S ∈ I, and (3) α ∈ I iff α′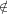 I,
for any α ∈ B (where ”∨
” and ”∧
” denote arbitrary meets and joins respectively, in
B).
I,
for any α ∈ B (where ”∨
” and ”∧
” denote arbitrary meets and joins respectively, in
B).
The denotation of the expression α, with its specified category will be noted [α] and we
will be interested only in the extensional aspects of the meaning. If α is a V P which
denotes the set P, a subset of the universe, then αR, raised α, denotes a set of type ⟨1⟩
quantifiers:
(5) [αR] = {Q : Q(P) = 1}, where Q is a type ⟨1⟩ quantifier.
The set of type ⟨1⟩ quantifiers, associated with the property P, defined in (5) is particular because its characteristic function is a homomorphism from the algebra of type ⟨1⟩ quantifiers to the algebra of truth-values. It follows from this that the set in (5) corresponds to the individual on the algebra DNP generated by the atomic quantifier QP. Such individuals, that is individuals on the algebra DNP generated by atomic (type ⟨1⟩) quantifiers will be called verbal individuals. One can see that any verbal individual has at least one nominal individual as a member. Furthermore, a verbal individual is in particular a complete set of quantifiers (every type ⟨1⟩ quantifier or its Boolean complement belong to the set) and it is consistent (no quantifier and its Boolean complement belong to it).
Given the fact that the denotational algebra of (non -raised) VPs and of characteristic functions of verbal individuals are isomorphic we can say that ”classically” VPs denote (up to the isomorphism) verbal individuals. In this paper we consider a more general case: we suppose that there is the denotational algebra DV PR, which is the set of functions from DNP to the algebra {0,1}. and these functions need not to be homomorphisms. This lack of homomorphism property will be the basic semantic property of the constructions that will be considered.
Since our basic argument for the necessity of raised verb phrases uses transitive
VPs with special direct objects we need to specify how the composition between
the transitive verb and its second argument - the direct object, is realised. I will
follow here the well-justified proposal in Keenan (2016) who indicates various
merits of the interpretation of the direct objects in situ, as functions taking binary
relations - denotations of transitive verbs, as arguments. Thus Keenan proposes
that direct object NPs are of the category (S∕NP)∕((S∕NP)∕NP). Formally, at
the semantic level, this is done by extending the domain of type ⟨1⟩ quantifiers:
in addition to sets, the basic domain of type ⟨1⟩ quantifiers, relations are also
considered as their possible arguments. Thus type ⟨1⟩ quantifiers, considered as
functions, can apply not only to sets but also additionally to relations - denotations of
transitive (ditransitive, etc.) verbs. When such functions with the extended domain
act as denotations of direct object they are accusative extensions Qacc of the
quantifier Q, defined in D2 (i) and when they act as denotations of subjects (NPs in
nominative case) of transitive sentences they are nominative extensions defined in D2
(ii):
D2 (i): For each type ⟨1⟩ quantifier Q, QaccR = {a : Q(aR) = 1}
(ii) For each type ⟨1⟩ quantifier Q, QnomR = {a : Q(Ra) = 1, where aR = {y : ⟨a,y⟩∈ R}
and Ra = {y : ⟨y,a⟩∈ R}.
The nominal extension of a quantifier can be used to represent readings of transitive sentences with the object wide-scope (Keenan 2016).
Nominal and accusative case extensions are specific type ⟨2 : 1⟩ functions. One can
distinguish various kinds of type ⟨2 : ⟨1⟩⟩ and type ⟨1,2 : ⟨1⟩⟩ functions. Observe first that
any type ⟨2 : 1⟩ function whose output is denoted by a (non-raised) VP can be lifted to a
type ⟨2 : ⟨1⟩⟩ function. The accusative extension of a type ⟨1⟩ quantifier Q can be lifted to
type ⟨2 : ⟨1⟩⟩ function in the way indicated in (6). Such functions will be called accusative
lifts. More generally, if F is a type ⟨2 : 1⟩ function, its lift FL, a type ⟨2 : ⟨1⟩⟩ function, is
defined in (7):
(6) QaccL(R) = {Z : Z(Qacc(R)) = 1}.
(7) FL(R) = {Z : Z(F(R)) = 1}.
The variable Z above runs over the set of type ⟨1⟩ quantifiers.
We will also use two types of set partitions, defined by the binary relation R. First, if R is an irreflexive symmetric relation (i.e. R ∩ R−1 ∩ I = ∅) then Π(R) is the least fine partition of R such that each of its blocks is of the form (A × A) ∩ I′. A partition is trivial iff it contains only one block. Observe that if R is an irreflexive symmetric relation and Π(R) is not trivial, then every block of Π(R) contains at least two elements.
Second, to analyse the sentences with the same CN and the same number of CN we will
use partitions induced by the following equivalence relations associated with the binary
relation R:
D3 (i) eR = {⟨x,y⟩ : xR = yR}
(ii) eR,n = {⟨x,y⟩ : |xR| = |yR|}
To show that it is necessary to raise the type of VPs to get right semantics of some
constructions I will indicate some semantic properties of these constructions and show that
they are incompatible with properties held by non-raised VPs. For non-raised VPs the
following is true: sentences of the form in (8a) are equivalent to sentences of the form
(8b):
(8a) (NP1 V P) and (NP2 V P)
(8b) (NP1 and NP2) V P
In other words if NP1 denotes the quantifier Q1, NP2 denotes the quantifier Q2 and
V P denotes the property P then (9) holds:
(9) (P ∈ Q1 ∧ P ∈ Q2) ≡ P ∈ (Q1 ∩ Q2)
The property in (9) is a consequence of the fact that quantifiers denoted by the subject NPs are homomorphisms from the algebra of sets (subset of a given universe) to the algebra of truth values. This property will be frequently used as a test to check whether a certain type of a VPs denotes or not a set. It will be called homomorphism test or h-test.
In the same way for type ⟨2 : ⟨1⟩⟩ functions which are lifts of type ⟨2 : 1⟩ functions we
have:
Proposition 1: If a type ⟨2 : ⟨1⟩⟩ function F is a lift of a type ⟨2 : 1⟩ function then for any
type ⟨1⟩ quantifiers Q1 and Q2 and any binary relation R, if Q1 ∈ F(R) and Q2 ∈ F(R)
then (Q1 ∧ Q2) ∈ F(R)
Accusative lifts satisfy the following higher order extension condition HEC (Zuber
2014):
D4: A type ⟨2 : ⟨1⟩⟩ function F satisfies HEC (higher order extension condition) iff for any
natural type ⟨1⟩ quantifiers Q1 and Q2 with the same polarity, any A,B ⊆ E, any binary
relations R,S, if Li(Q1,A), Li(Q2,B) and ∀a∈A∀b∈B(aR = bS) then Q1 ∈ F(R) iff
Q2 ∈ F(S).
For functions satisfying HEC we have:
Proposition 2: Let F satisfies HEC and let R = E ×C, for C ⊆ E arbitrary. Then for any
X ⊆ E either Ft(X) ∈ F(R) or for any X, Ft(X)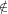 F(R)
F(R)
Thus a function satisfying HEC condition and whose argument is the cross-product
relation of the form E ×A, has in its output either all principal filters or no principal filter.
Thus Proposition 2 can be used to show that the function denoted by each other and by
other expressions which induce the VP raising, do not satisfy HEC. Functions denoted by
such expressions satisfy conditions which are strictly weaker than HEC. Thus the
denotations of higher order anaphors satisfy the the higher order predicate invariance or
HPI. By definition (Zuber 2014):
D5: A type ⟨2 : ⟨1⟩⟩ function F satisfies HPI (higher order predicate invariance) iff for type ⟨1⟩ quantifier Q, any A ⊆ E, any binary relations R,S, if Li(Q,A) and ∀a∈A(aR = aS) then Q ∈ F(R) iff Q ∈ F(S).
An equivalent way to define HPI is given in:
Proposition 3: Function F satisfies HPI iff if Li(Q,A) then Q ∈ F(R) iff
Q ∈ F((A × E) ∩ R)
Similarly, higher order comparatives satisfy the so-called higher order argument
invariance or HAI (Zuber 2014):
D6: A type ⟨2 : ⟨1⟩⟩ function F satisfies HAI (higher order argument invariance) iff for any
natural type ⟨1⟩ quantifiers Q1 and Q2 with the same polarity, any A,B ⊆ E, any binary
relation R, if SLi(Q1,A), SLi(Q2,B) and ∀a∈A∀b∈B(aR = aS) then Q1 ∈ F(R) iff
Q2 ∈ F(R).
Obviously HEC entails both HPI and HAI.
The first class of VP raising inducers we discuss, in some sense the most important one, is
represented by proper GNPs. We start by indicating differences in entailments between
sentences with ordinary NPs in the direct object position and sentences with
proper GNPs on the direct object position. We observe that the former sentences,
in contradistinction to the latter, pass the h-test. Consider first the following
examples:
(10a) Leo and Lea hug ten/most students.
(10b) Bill and Sue hug ten/most students.
(11) Leo, Lea, Bill and Sue hug ten/most students.
It is easy to see that (10a) in conjunction with (10b) entails (11). This is not surprising
given the property in (9) and the fact that the VPs in (10a) and (10b) denote sets.
However, sentences with proper GNPs in the object position behave differently in this
respect as shown in the following examples:
(12a) Leo and Lea hug each other/each other and Kim.
(12b) Bill and Sue hug each other/each other and Kim.
(13) Leo, Lea, Bill and Sue hug each other/each other and Kim.
(14a) Leo and Lea read the same book/the same five books.
(14b) Bill and Sue read the same book/the same five books.
(15) Leo, Lea, Bill and Sue read the same books/the same five books.
Clearly (12a) in conjunction with (12b) does not entail (13). Similarly, (14a) in conjunction with (14b) does not entail (15). In the same way (12a) and (12b) do not entail that four persons hug each other and (14a) and (14b) do not entail that four persons read the same book. This means that the functions denoted by the subject NPs in (14a) and (14b) do not apply to the predicate denoted by the complex VPs in these sentences and the conjunction and is not understood pointwise. Furthermore, given property in (9) and proposition 1 this means that the VPs in the above sentences do not denote properties and that the objects of these sentences do not denote lifts of type ⟨2 : 1⟩ functions.
Another thing one observes looking at transitive sentences with GNPs as direct object is
that they can have virtually any plural NP as their grammatical subject. Thus the
following are all acceptable sentences:
(16) Kim and Leo/most students/three teachers/no two monks admire each other.
(17) Between five and ten students/some philosophers read the same book.
In the above sentences GNPs form with the transitive verb a V P, which is a ”natural” constituent. Hence, to avoid the type mismatch and get the right interpretations we will consider that the GNPs each other, each other and Kim, the same books and the same five books denote genuine higher order functions on binary relations that is functions of type ⟨2 : ⟨1⟩⟩.
It is important to keep in mind that there are ”many” proper GNPs which have similar behaviour in transitive sentences. For instance all Boolean compounds of each other with ordinary NPs or with the reflexive himself such as each other and most teachers or each other, themselves and Dan form such anaphoric GNPs. Similarly reciprocal determiners (cf. Zuber 2016) such as every... except each other or most... in addition to each other when applied to common nouns give anaphoric GNPs with similar semantic properties.
There are also ”many” comparative GNPs giving rise to similar differences in the
entailment. This is the case, for instance, with Boolean compounds such as the same books
and five articles or the same five students and one teacher. In addition higher order
comparative GNPs can be formed with other ”comparative” determiners such as similar,
very similar, different, almost the same, almost the same number of, the same kind of,
comparable, interchangeable, related, analogous etc. These determiners can also Booleanly
combine between them and the GNPs they form with CNs in their turn can form
Boolean compounds. The following examples illustrate some of these possible
compounds:
(18) Leo and Dan admire most linguists, except themselves and each other.
(19) Most logicians know the same five and ten different theorems.
(20) No two philosophers admire each other and Plato.
(21) Some students admire each other and the same teachers.
(22) Most Japanese drive very similar cars.
(23) They read the same articles and Exciting Logic.
An entailment test similar to the one applied to sentences (14a) and (14b) indicates that h-test can be applied here to all the above sentences and thus the VPs in these sentences do not denote sets.
I will provide now the semantics for the anaphoric GNPs each other and for the comparative GNP the same CN using the fact that the VPs they form with transitive verbs are of the category S∕(S∕(S∕NP)). The semantics of some other anaphoric GNPs is given in Zuber (2016) and the semantics of some other higher order comparative NPs is given in Zuber (2017). The functions defining the semantics of each other and of the same CN are important for what follows because they are used to define the semantics of other constructions which induce the VP raising.
Functions corresponding to the semantics of each other and the same CN use partitions
defined above. To define the type ⟨2 : ⟨1⟩⟩ function EA denoted by the reciprocal each other
we use the partition Π(RS−) (Zuber 2016). This definition is a definition ”by
cases” which depends on whether the partition Π(RS−) is trivial or non-trivial.
Thus:
D7: (i) EA(R) = {Q : Q ∈ PL ∧¬2(E) ⊆ Q} if RS− = ∅
(ii) EA(R) = {Q : Q ∈ PL ∧ QD(B) ⊆ Q}, if Π(RS−) is trivial with B as its only
block
(iii) EA(R) = {Q : Q ∈ PL∧∃B(B ∈ Π(RS−)∧Q(D(B) = 1}∪{Q : Q ∈ PL∧∃B(B ∈ Π(RS−)∧Q = ¬QD(B)}
if Π(RS−) is non-trivial.
The meaning of each other defined in D7 corresponds to strong logical reciprocity. Weaker reciprocity can be obtained by taking into consideration in D7 some subsets of the relation RS−.
As the second example of a GNP which forces raising of the VP we give the semantics of the comparative GNP the same CN. Strictly speaking we specify the function SAME(X,R), denoted by the (generalised) determiner the same. We consider that this determiner denotes a type ⟨2,1 : ⟨1⟩⟩ function. To define this function we use the partition ΠRX(E) corresponding to the equivalence relation eRX, defined in D2 (ii). This again is a definition ”by cases”. The output of the function to be defined, is a set of plural type ⟨1⟩ quantifiers, which is denoted by the raised VP, will in general contain three parts: positive, negative and ”atomic”. The positive part corresponds, roughly, to the set of quantifiers true of some block of the partition and the negative part corresponds to the set of quantifiers that are false of sets which are not blocks of the partition.
We will say that the block of a partition is singular if it is a singleton. A block B is
plural, B ∈ PL, if it is contains at least two elements. A partition is atomic iff all its blocks
are singular. With the help of these notions, using the partition ΠRA(E) we can now
express the function SAME(X,R), where R is a non-empty binary relation, and X a
non-empty set, as follows (Zuber 2017):
D8: SAME(X,R) =
(i)={Q : Q ∈ PLR ∧¬2(E) ⊆ Q}, if ΠRX(E) is atomic
(ii)= {Q : Q ∈ PLR ∧∃B(B ∈ ΠRX(E) ∧ B ∈ PL ∧ Q(B) = 1)}∪
{Q : Q ∈ PLR ∧∃C⊆E∀B∈ΠR
X(E)(C ⁄⊆ B ∧¬ALL(C) ⊆ Q)}, if ΠRX(E) is not
atomic.
The above definition says that SAME applied to a set X and a binary relation R gives as result a set of quantifiers, as desired. This set can be decomposed into various sub-sets depending indirectly on the ”content” of the relation R and thus on the partition of E induced by R and X. According to the clause (i), when the partition is atomic then no two objects are in the relation R with all objects of a sub-set of X. This entails in particular that the quantifier denoted by no two objects and any of its consequences belong to the set SAME(X,R). This means that, for instance, the quantifiers denoted by no five objects or no two students also belong to the set SAME(X,R).
Clause (ii) concerns the case where the partition is not atomic. In this case there is at least one plural block of the partition such that all its members are, roughly speaking, in the relation R with the same subset of X. This block corresponds to the property expressing the sameness we are looking for and a plural quantifier can be true or false of it. The second part of the clause (ii) provides a set of quantifiers obtained from a ”negative information” given by sets which are not blocks of the partition. If, for instance, Jiro and Taro are Japanese students who read different books then no set to which they belong is a block of ΠRB(E) - where R corresponds to READ and B - to BOOK. Then, according to the second part of the clause (ii), the quantifiers denoted by the NPs not all Japanese students, not all students and not all Japanese belong to SAME(B,R).
To describe the function denoted by the (generalised) determiner the same number of we use the partition corresponding to the equivalence relation eR,n defined in D3(ii) above (cf. Zuber 2017).
Both functions, EA and SAME, have specific properties which make them different from any lift of a type ⟨1⟩ function. Using proposition 1 it is easy to show that they do not satisfy HEC in particular. Moreover, EA satisfies HPI and SAME satisfies HAI. In addition, these functions have other thing in common: in the description of their content the structure of the relations which are their arguments, in particular the partitions which can be induced by these relations, are explicitly taken into account.
In the preceding section the arguments for raising VPs were based on constructions in which special verbal arguments apply to transitive VPs and give as result raised VPs denoting sets of type ⟨1⟩ quantifiers. In this section I discuss briefly a somewhat different case of VPs which have to be raised but which are not formed from transitive verbs. Here one can distinguish two cases: the case of a raised VP which does not contain any modifier inducing the raising and the case of an intransitive VP which does.
I start with the intransitive (”on the surface”) verbs which express symmetric relations,
such as to meet or to argue (and not to meet with or to argue with) or the predicates such
as to live on the same street or to be an enemy (and not to live on the same street as or to
be an enemy of ). As it has been often noted subject NPs of sentences with such
symmetric predicates have to be interpreted ”collectively” since the ”property” they
express cannot in general apply to individuals, as shown in the following examples
:
(24a) Leo and Lea met (in the park).
(24b) *Leo met.
(25a) Most teachers met.
(25b) *A student met.
(26) ?Leo is an enemy.
On the other hand, sentences with VPs representing symmetric predicates do not pass
the h-test: for instance using (24a) and (27) as premisses one cannot obtain (28) as
conclusion:
(27) Bill and Dan met.
(28) Leo, Lea, Dan and Bill met.
The verb to meet and the predicate to live on the same street are interesting in addition
for another reasons: as indicated above they are among the predicates that admit implicit
or optional arguments. An item which can take a complement is an item with an optional
complement if it can occur in a sentence with or without its complement and
thus the omission of the complement in a acceptable sentence does not lead to
the unacceptability of the sentence, but may lead to some meaning changes. In
particular verbs with optional arguments can occur as intransitive, transitive,
or verbs with oblique objects. The verb to meet in English in addition to being
intransitive can take direct and indirect objects. Similarly with other symmetric
predicates. In this respect they resemble verbs with GNPs in the form of higher order
comparatives:
(29) Leo met Lea.
(30) Leo met with Lea.
(31) Leo read the same book as Lea.
Words with optional complements pose various challenges for formal semantics, one of them being their categorial and lexical ambiguity (Gillon 2012). One can notice that (24a) has two forms logically equivalent to it, with ”the same verb” taking either direct object as in (29) or an indirect object (in ”comitative case”) as in (30). In these sentences with explicit verbal arguments the VPs express a (first order) property and sentences with such VPs and plural NP subjects can have distributive meaning in opposition to the corresponding sentences with omitted verbal arguments.
The semantics of sentences with verbs expressing symmetric relations but in
which the complements are omitted necessitates their raising. Given, however
the fact that such sentences are in general equivalent to corresponding sentences
with each other or the same we know already how to compute their meaning.
For instance (27) can be considered as logically equivalent to (32) and (33a) to
(33b):
(32) Leo and Lea met each other.
(33a) Lea and Dan married.
(33b) Lea and Dan married each other.
As the following examples show not all verbs with implicit complements express
symmetric relations:
(34) Leo and Lea undressed.
(35a) Leo and Lea undressed themselves.
(35b) Leo and Lea undressed each other.
(36) Leo and Lea kissed.
(37) Leo and Lea kissed each other.
Verbs to undress and to kiss are verbs in which arguments are optional and thus they can occur either as intransitive verbs or transitive verbs. Sentence in (34) entails neither (35a) nor (35b) and the one in (36) means, for pragmatic reasons only (37). The representations of the ”mixed” (reflexive-reciprocal) reading of (34) and of the reciprocal reading of (36) necessitates raising of the intransitive verbs to undress and to kiss.
One of the consequences of the above observations is that verbs admitting omitted arguments can take their denotations in three different denotational algebras: in DS∕NP)∕NP, in DV P and in DV PR. This situation is similar to the one one finds with some NPs which can also denote in three different types (Partee 1987).
Let us see now some examples of constructions where raising is induced by some verbal
modifiers (that is adverbial phrases) and not by verbal arguments. Before introducing
adverbs which force the raising of VPs, it is important to observe that they do not belong
to the class of ”classical” adverbs of quantification with non-nominal domain forming
adverbials or prepositional phrases. For instance (non-nominal) quantifiers such as always,
everywhere, never, nowhere, often, most of the time, on some occasions etc. do not force
VP raising. Sentences with these adverbs do pass the h-test: (38) and (39) together entail
(40):
(38) Dan never drinks.
(39) Most monks never drink.
(40) Dan and most monks never drink.
A good candidate for an adverb forcing the raising of the VP is the adverb together.
Detailed semantics of this adverb may involve various aspects (cf. Moltmann 2004) which
will not be discussed here. Consider the following examples:
(41a) Kim and Dan left together.
(41b) Leo and Lea left together.
(42) Kim, Dan, Leo and Lea left together.
One observes that the above sentences behave like transitive sentences with GNPs and sentences with omitted verbal arguments. Thus (41a) in conjunction with (41b) does not entail (42). This means, according to Proposition 1 that the type of the object denoted by the VP left together is different from ⟨e,t⟩.
Sentences with VPs modified by the adverb together can also take as subject virtually
any plural NP in the same way as transitive sentences containing a proper GNP as direct
object:
(43) Some/most/ten students/Leo and Kim left together.
It is worth recalling that in many languages the ”reciprocal morpheme” which gives rise to proper GNPs with the reciprocal meaning we discussed above, can have many uses and carry multiple ”meanings” (Lichtenberg 1985). In particular in languages related to Turkish this morpheme can carry the so-called social or associative meaning expressed in English by the adverbial together. So it should not be surprising that there are adverbials forcing type raising of VPs even if they are categorially different from nominal verbal arguments discussed in the preceding section.
For present purposes it is enough to notice that (41a) can be considered as equivalent to
(44):
(44) Kim and Dan left with each other.
In this case left with can be considered as expressing a binary relation and thus the raising of the VP is necessary because of the presence of the GNP each other.
The situation is probably more complicated in (43). Very likely in this case we need a ”weaker” together: it is not necessary that any member of the group of ten students or of the group representing the majority of students leaves with every other member of the group. In other words together in (43) should be defined by weaker each other.
An adverb related to together is the adverb separately. One can check that sentences with VPs modified by this adverb do not pass the i-d- test and thus this adverb also induces VP-raising. Similarly, adverbs related to the same such as in the same way, equally, differently, etc. induce VP raising. Thus to get the semantics of the VPs such as argue in the same way, be equally stupid and dress differently we have to raise their type.
Gerundives in many languages can act as VP modifiers, as for instance in to dance
singing and laughing or to sit reading a book. It seems natural to consider that gerundives
used as modifiers of VPs and formed from raised VP force the raising of the VP which they
modify:
(45) Leo and Lea came using the same taxi.
(46) Lea and Dan left kissing each other.
To obtain the semantics of the above sentences the VPs have to be raised. I will not
show this in detail since, in particular, it involves the semantics of gerundives in general.
It suffices to notice that in many cases gerundival adverbials can be expressed
by the conjunction of the modified VP with the one from which the gerundive
is formed. For instance (47) can be considered as being logically equivalent to
(48):
(47) Lea and Dan were dancing talking to each other.
(48) Lea and Dan were dancing and talking to each other.
Recall that one of the arguments for NP raising is based on Boolean compounds. This argument is related to the use of proper nouns in Boolean compounds with quantified NPs: roughly speaking, in order to compute the meaning of such compounds all members of the compound have to denote in the same type and thus the type of the proper nouns has to be lifter from e to ⟨⟨e,t⟩,t⟩. The same argument applies in the case of the VP raising: one cannot conjoin, for instance, a raised VP and a non-raised one if one wants to compute the meaning of the whole conjunction.
The argument for the VP raising based on Boolean compounds applies not only to cases
with gerundival modification. Consider the following examples:
(49) Leo and Lea left and took the same taxi.
(50) Most students danced, sang the same song and held each other’s hands.
(51) Some monks met and discussed jokes.
Although the semantics of the first VPs in (49) and in (50) can be given without raising them when they are in isolation, being conjoined with raised VPs in these sentences they too must be raised. Similarly, in (51) the VP discussed politics must be raised since it occurs in a conjunction with the raised VP met.
The fact that some adverbs inducing the raising can be ”described” with the help of
GNPs such as each other and the same allows us to see in a different light some hard
problems related to the semantics of cumulative readings of some quantifiers in specific
contexts. When one thinks about the famous example of piano lifters it becomes obvious
that the cumulative reading entails that the lifters lifted the piano with each other and the
it was the same piano. In fact, strictly speaking, the same in case is weaker than the same
defined in D13 because it only inverses the scope of the direct object (Zuber 2017). Thus
the meaning of (52a), with the cumulative interpretation of its subject NP, can
be expressed by something like (52b). Similarly, (53a) can be ”translated” by
(53b):
(52a) Leo and Dan lifted the piano.
(52b) There is a piano such that Leo and Dan lifted it together.
(53a) Three philosophers wrote nine articles (for the journal).
(53b) There are nine articles (of the journal) such that three philosophers wrote them
together.
The presence of the modifier together, taken possibly in its weak reading, in the above sentences is essential. In general both, subject and object, NPs in cumulative readings are scopeless but in this case the presence of together allows for such a representation with the object NP taking wide scope.
In fact to have cumulative/collective readings both the adverbial together and
the comparative the same have to occur: (54a) does not and (54b) expresses a
collective/cumulative action:
(54a) Leo and Dan read the same book.
(54b) Leo and Dan read the same book together.
The example in (54b) shows that functions forcing VP raising may be predicate and argument invariant ”at the same time”.
I conclude this section by indicating that the so-called categorially polyvalent modifiers such as only, even, also, etc. can also be considered as inducing VP raising when they have in their scope intransitive VPs. This point will not be developed here.
One of the most often used applications of type raising is related to the difficulty of dealing with the semantics of ”plural” NPs. In fact one can notice that even ”simple” sentences which have as the subject NP a conjunction of two proper nouns and the VP marked by the plural verbal marker, do not pass the h-test. For this reason many operators defining specific raisings NPs, or even of the (nominal) determiner forming a NP, have been proposed. In this paper I advocate for the usefulness of the ”classical raising” strictly related to Montagues’s NP raising without any additional ”non-classical” raising of determiners. It can be defined by set-theoretical (type theoretical) means. Such VP raising is necessary for the compositional semantics of various complex predicates whose readings are difficult, if not impossible, to be expressed in first order logic.
No formal results concerning VP raising have been presented. At least two kind of questions related to formal properties have to be investigated. The first concerns the constraints that should be imposed on the content of raised VPs and on the operation leading to it. We have seen that sets of quantifiers denoted by properly raised VPs are not verbal individuals because they are closed with respect to meets. It seems, however that any set of quantifiers denoted by a properly raised VP is increasing in the sense that if a quantifier Q1 belongs to it and Q1 ⊆ Q2 then Q2 also belongs to it. For instance we see that (13) above entails (12a) and (12b), Similarly (15) entails (14a) and (14b).
All examples we have discussed essentially involve the plurality of the subject NPs in sentences with a raised VP. It seems thus obvious that individuals should be in some way excluded from the set of quantifiers corresponding to a raised VP and make part of the constraint on raising. The set of quantifiers denoted by properly raised VP should also be consistent. Less obvious is the constraint of completeness. We have seen that raised predicates involve plurality and so probably nominal individuals should be excluded from their denotations in some way. However, it is not clear whether such plural predicates with singular subject NPs should be considered as non-grammatical or just give rise to false sentences.
The second point concerns the status of other operations which go together with the classical raising, like for instance the operation of lowering a raised VP. For instance we need to know when, if ever, and why, a raised VP can be lowered in order to get its primitive type ⟨e,t⟩. More specifically we want to know under what conditions to a given set ◇V P of type ⟨1⟩ quantifiers one can associate by an operation, which is the inverse to the VP raising, a set (of individuals) such that by raising this set we get the given set ◇V P of quantifiers. Recall that in the case of the ”classical” NP raising the corresponding inverse operation is a mapping LOW from type ⟨1⟩ quantifiers to elements to E. More precisely it is a partial mapping which applies to nominal individuals, treated as quantifiers (principal ultrafilters) and maps such quantifiers to their generators (Partee 1987). The situation is quite similar in the case of the VP raising: any set of type ⟨1⟩ quantifiers which ia a verbal individual can be lowered to a set. This set is obtained by taking the meet of all nominal individuals members of the given verbal individual. Of course only sets of quantifiers which are verbal individuals can be lowered in this way. For instance for any binary relation R and any type ⟨2 : 1⟩ function F, the set FL(R) of type ⟨1⟩ quantifiers (where FL is defined as in (7)) can be lowered: LOW(FL(R)) = F(R).
Another series of questions related to the VP raising concerns its complexity
and possible strategies for processing sentences with raised VPs. Van Benthem
(1984) proposes to measure the semantic complexity of types by the function o of
order which assigns to any type a natural number. It is defined recursively as
follows:
(55) (i) o(e) = o(t) = 1
(ii) o(⟨a,b⟩) = max(o(a) + 1,o(b))
Given this measure the complexity the type of raised VPs is of order 3. This order is not higher than the order of the type of (nominal) determiners (type ⟨⟨e,t⟩,⟨⟨e,t⟩,t⟩⟩) or the type of prepositions (type ⟨⟨⟨e,t⟩t⟩,⟨⟨e,t⟩,⟨e,t⟩⟩). Van Benthem indicates that order 3 is sometimes considered as the threshold for natural languages. Given the fact that the order of raised VPs is 3, one can consider that the operation of VP raising does not go beyond this threshold. It is not clear, however, what are the consequences of this fact for the way sentences with raised VPs can be processed.
[1] Bach, E. (1980) Tenses and aspects as functions on verb phrases, in Ch. Rohrer (ed.) Time, Tense, and Quantifiers, Tuebingen: Niemeyer, pp. 19-37
[2] van Benthem, J. (1986) Essays in Logical Semantics, Reidel Publishing Company
[3] Van der Does (1993) Sums and Quantifiers, Linguistics and philosophy 16, pp. 509-550
[4] Geach, P. (1972) A Program for Syntax, in Davidson, D. and Harman, G. (eds.) Semantics of Natural Language, Reidel, Dordrecht
[5] Gillon, B. S. (2012) Implicit complements: a dilemma for model theoretic semantics, Linguistics and Philosophy 35, pp. 313-359
[6] Humberstone, L. (2005) Geach’s Categorial Grammar, Linguistics and Philosophy, 28, pp. 281-317
[7] Keenan, E. L. (2016) In Situ Interpretation without Type Mismatches, Journal of Semantics 33:1, pp. 87-106
[8] Keenan, E. and Faltz L. (1985) Boolean Semantics for Natural Language, Reidel Publishing Company
[9] Keenan, E. L. and Westerståhl, D. (1997) Generalized Quantifiers in Linguistics and Logic, in van Benthem, J. and ter Meulen, A. (eds.) Handbook of logic and language, Elsevier, Amsterdam, pp. 837-893
[10] Lichtenberk, F. (1985) Multiple uses of reciprocal constructions, Australian Journal of Linguistics 5: 19-41
[11] Lønning, J. T. (1997) Plurals and Collectivity, in van Benthem, J. and ter Meulen, A. (eds.) Handbook of logic, and language, Amsterdam: Elsevier, pp.1009-1054
[12] Moltmann, F. (2004) The semantics of together, Natural Language Semantics 12: pp. 289-318
[13] Montague, R. (1973) The proper treatment of quantification in ordinary English, in J. Hintikka et al. (eds) Approaches to natural language: proceedings of the Stanford workshop on Grammars and Semantics, Dordrecht, Reidel, Reprinted in Montague 1974, pp. 247-270
[14] Montague, R. (1974) Formal Philosophy: selected papers of Richard Montague, edited and with an introduction by Richmond Thomason. Yale University Press
[15] Partee, B (1987) Noun Phrase Interpretation and Type-Shifting Principles, in Groenendijk J. et al (eds) Studies in Discourse Representation Theory and the Theory of Generalized Quantifiers, Foris, Dordrecht, pp. 115-143
[16] Partee, B. and Rooth, M. (1983) Generalized conjunction and type ambiguity, in Bauerle, R. et al.(eds) Meaning, Use, and Interpretation of Language, Berlin: de Gruyter, 361-383
[17] Winter, Y. (2001) Flexibility principles in Boolean semantics, London: The MIT Press
[18] Zuber, R. (2014) Generalising Predicate and Argument Invariance, in Asher, N. and Soloviev, S. (eds) Logical Aspects of Computatioonal Linguistics, LACL 2014 Proceedings, Springer, pp.163-176
[19] Zuber, R. (2016) Anaphors and Quantifiers, in V
 n
n nen, J. et al. (eds.)
Logic, Language, Information, and Computation, Springer, pp. 432-445
nen, J. et al. (eds.)
Logic, Language, Information, and Computation, Springer, pp. 432-445
[20] Zuber, R. (2017) Set Partitions and the Meaning of the Same, Journal of Logic, Language and Information 26, pp.1-20
[21] Zuber; R. (forthcoming), On generalized noun phrases, forthcomong in A. Foret, R. Muskens and S. Pogodalla (eds.) Formal Grammar 2017, Springer Verlag